The asymptotic behavior for a binary alloy in energy and material science: The unified method and its applications

M. Adel; K. Aldwoah; F. Alahmadi; M.S. Osman

doi:10.1016/j.joes.2022.03.006

Journal of Ocean Engineering and Science >

2024 , Vol. 9 >Issue 4: 373 - 378

DOI: https://doi.org/10.1016/j.joes.2022.03.006

Original article

The asymptotic behavior for a binary alloy in energy and material science: The unified method and its applications

M. Adel ^,^a ,
K. Aldwoah ^,^a ,
F. Alahmadi ^,^a ,
M.S. Osman ^,^b

Expand

^a Department of Mathematics, Faculty of Science, Islamic University of Madinah, Medina, Saudi Arabia
^b Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt

Received date: 2022-02-10

Revised date: 2022-03-04

Accepted date: 2022-03-10

Online published: 2024-08-13

Fold

Abstract

The Cahn-Hilliard system was proposed to the first time by Chan and Hilliard in 1958. This model (or system of equations) has intrinsic participation energy and materials sciences and depicts significant characteristics of two phase systems relating to the procedures of phase separation when the temperature is constant. For instance, it can be noticed when a binary alloy (â€œAluminum + Zincâ€ or â€œIron + Chromiumâ€) is cooled down adequately. In this case, partially or totally nucleation (nucleation means the appearance of nuclides in the material) is observed: the homogeneous material in the initial state gradually turns into inhomogeneous, giving rise to a very accurate dispersive microstructure. Next, when the time scale is slower the microstructure becomes coarse. In this work, to the first time, the unified method is presented to investigate some physical interpretations for the solutions of the Cahn-Hilliard system when its coefficients varying with time, and to show how phase separation of one or two components and their concentrations occurs dynamically in the system. Finally, 2D and 3D plots are introduced to add more comprehensive study which help to understand the physical phenomena of this model. The technique applied in this analysis is powerful and efficient, as evidenced by the computational work and results. This technique can also solve a large number of higher-order evolution equations.

Highlights

● Different wave structures for abundant solutions to the Chan–Hilliard system are investigated.

● Performance was done using the strategy of the unified method.

● Physical explanations are discussed for the obtained solutions.

Key words： Cahn-Hilliard system; Traveling wave solutions; The unified method; Variable coefficients

Cite this article

M. Adel , K. Aldwoah , F. Alahmadi , M.S. Osman . The asymptotic behavior for a binary alloy in energy and material science: The unified method and its applications[J]. Journal of Ocean Engineering and Science, 2024 , 9(4) : 373 -378 . DOI: 10.1016/j.joes.2022.03.006

1. Introduction

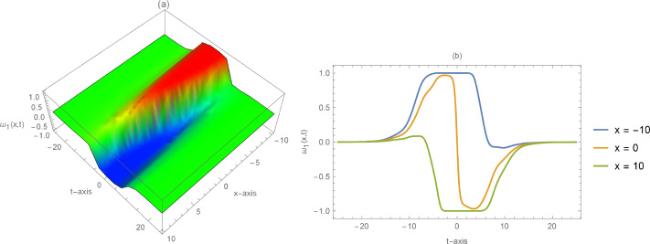
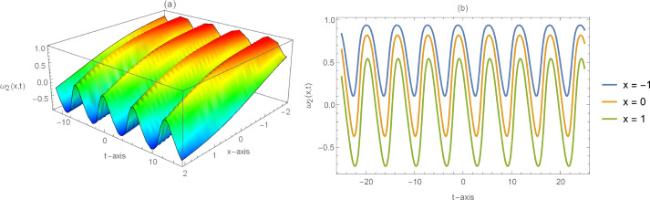
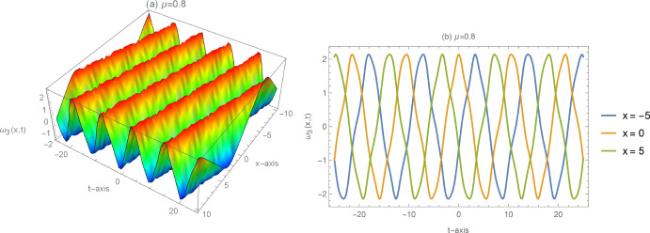
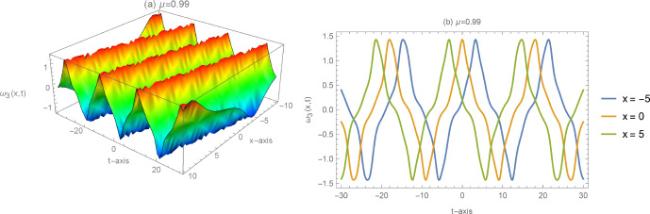
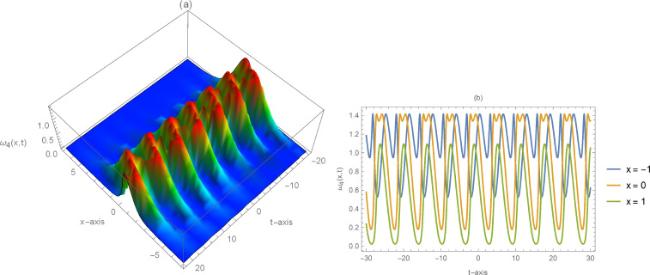
Nonlinear evolution equation is a research hotspot in different fields of science and engineering especially in energy and material science topics [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14]. No doubt experts have made remarkable achievements in these fields. So far, a variety of analytical and numerical schemes have been introduced to analyze and solve nonlinear evolution equations (NLEEs), the most typical of which include the unified method and its generalized form [15], [16], the tanh-coth-expansion and sine-cosine-function methods [17], [18], the

(G^{'} / G)

-expansion method [19], [20], [21], sine-Gordon expansion method [22], [23], the modified Kudryashov method [24], [25], [26], the Hirota bilinear method [27], [28], [29], [30], [31], the finite difference method [32], the Riccati equation technique [33], the modified reproducing kernel discretization technique [34], the long wave limit method [35], the cubic B-spline scheme [36], the q-homotopy analysis [37] and the bilinear neural network method [38], [39], [40], [41]. In this research, we examine the dynamical behavior of a minor element achieved through the phase decomposition of the main element in a binary alloy which is completely described by the Cahn-Hilliard (CH) system [42], [43] via the unified method [44], [45], [46]. To this end, many exact solutions are created for this model and the physical meanings for the obtained solutions are illustrated by two- and three-dimensional figures and their contour plots.

The use of the CH equations for binary alloys of

(F e - C r)

and

(F e - X)

can locate gradient energy and mobility [47], [48]. In this case, the model can be represented as follows:

(1)

\begin{matrix} {(Υ_{i})}_{t} + D_{i} {(Υ_{i})}_{x x} + μ_{i} κ_{i} {(Υ_{i})}_{x x x x} = 0, \end{matrix}

where

Υ_{i} = {\begin{matrix} Υ_{C r} \\ Υ_{X} \end{matrix}

D_{i} = - μ_{i} {(ϖ_{i})}_{Υ_{i}^{2}}

μ_{i}

represents uphill diffusion, and

{(ϖ_{i})}_{Υ_{i}^{2}}

is the total free energy. Further, the CH equations can be written as

(2)

\begin{matrix} {\begin{matrix} ω_{t} = \nabla \cdot μ (ω) \nabla [h (ω) - ϵ^{2} Δ ω], & (x, t) \in Ω \times ℜ^{+}, \\ n \cdot \nabla ω = n \cdot μ (ω) \nabla [h (ω) - ϵ^{2} Δ ω], & (x, t) \in \partial Ω \times ℜ^{+}, \end{matrix} \end{matrix}

where

h (ω)

represents the homogeneous free energy and

ϵ

is a constant. The system (2) admits the convective-diffusive CH equation [48]

(3)

\begin{matrix} ω_{t} = \nabla \cdot [μ (ω) \nabla (h {(ω)}_{ω} - κ \nabla^{2} ω)], \end{matrix}

where

ω (x, t)

and

μ (ω)

represent the concentration and the mobility, respectively. Consequently, Eq. (3) can be written in the next formula [47]

(4)

\begin{matrix} ω_{t} + D^{4} ω = D^{2} Γ (ω) + l D ω, l > 0, \end{matrix}

where

Γ (ω (x, t))

is a substantial chemical potential that has a common illustration as

(Γ (ω (x, t)) = ω^{3} (x, t) - ω (x, t))

and

ω (x, t)

denotes the concentration of one of two phases in a phase transitioning system.

l D ω (x, t)

, on the other hand, describes the phase shift caused by the fluid flow in a steady state. Eq. (4) covers the phase transition in binary systems such as glass and polymer mixtures as well as the kinetics of phase separation in iron-based ternary alloys.

Herein, The study of Eq. (4) is investigated when its coefficients are functions of the time. This discussion has attracted much attention rather than the constant case, since the majority of nonlinear physical equations in practice have variable coefficients. To this end we assume Eq. (4) with variable coefficients in the form:

(5)

\begin{matrix} ω_{t} + χ_{1} (t) D^{4} ω = χ_{2} (t) D^{2} Γ (ω) + l (t) D ω, l (t) > 0, \end{matrix}

where

χ_{1} (t)

χ_{2} (t)

and

l (t)

are real arbitrary functions.

The reminder of the article has been organized by the following next three Sections: Section 2 is dedicated to the unified method construction. The utilizing of the aforemention method on our problem and the analysis of the dynamical properties for the obtained solutions through some figures are investigated in Section 3, while Section 4 will contain the conclusion and results.

2. A short note on the unified method

In this part, we illustrate the algorithm of the unified method by introducing the following nonlinear differential equation with variable coefficients:

(6)

G (ω, ω_{t}, ω_{x}, ω_{t t}, ω_{x x}, \dots) = 0 .

Applying the wave transformation

η = α x + \int_{0}^{t} τ (t) d t, ω (x, t) = W (η)

into (6). Thus, Eq. (6) becomes an ordinary differential equation with the form:

(7)

\overline{G} (W, W^{'}, W^{″}, \dots) = 0,

where

α

is a real constant,

τ (t)

is an arbitrary function,

W = W (η)

and

W^{'} = \frac{d W}{d η}

The unified method classifies its solutions for Eq. (6) into two different categories namely: polynomial and rational forms with auxiliary functions that fulfil adequate auxiliary equations [44], [45], [46].

2.1. The polynomial type of wave solutions

This kind of solutions takes the following form

(8)

W (η) = \sum_{ı = 0}^{n} a_{ı} (t) {(ϑ (η))}^{ı},

where

a_{ı} (t)

are arbitrary functions in

t

and the auxiliary function

ϑ (η)

satisfies the following auxiliary equation

(9)

{(ϑ^{'} (η))}^{ϱ} = \sum_{j = 1}^{ϱ k} b_{j} (t) {(ϑ (η))}^{j}, ϱ = 1, 2,

where

b_{j} (t)

are arbitrary functions in

t

and

ϱ = 1

gives elementary or implicit solutions for Eq. (9), while

ϱ = 2

gives periodic or elliptic solutions. The homogeneous balancing requirement between the highest order derivative and highest nonlinear terms of Eq. (7) specifies the values of

n

and

k

when

ϱ = 1, 2

. We mention that the value of

k

depends basically on the parameters

s_{1}

s_{2}

and the highest derivative, say

s

, of Eq. (7). The parameter

s_{1}

is the total number of algebraic equations resulting from inserting Eqs. (8) and (9) into Eq. (7) and equating the coefficients of

ϑ (η)

with different powers identical zero. While, the parameters

s_{2}

represents the number of free parameters in Eqs. (8) and (9). Thus the condition for finding

k

is given by

s_{1} (k) - s_{2} (k) \leq s

when Eq. (7) is integrable.

2.2. The rational type of wave solutions

The unified method suggests the rational type of wave solutions as follow:

(10)

W (η) = \sum_{ı = 0}^{n} a_{ı} (t) {(ϑ (η))}^{ı} / \sum_{ℓ = 0}^{r} d_{ℓ} (t) {(ϑ (η))}^{ℓ}, n \geq r,

where

a_{ı} (t)

and

d_{ℓ} (t)

are arbitrary functions in

t

and the auxiliary function

ϑ (η)

satisfies the same auxiliary Eq. (9). The same technique in the previous case can be followed to obtain this type of solutions for Eq. (7).

In this work, we confine ourselves to discuss the solutions of Eq. (5) in the polynomial type. While the rational type solutions for this equation will investigate in a future work under the affect of the conformable derivative.

3. Solutions of Eq. (5) via the unified method

In the current part, we construct a variety of closed-form solutions with different structures for suggested Eq. (5).

To solve the model we have described, we apply the following wave transformation

ω (x, t) = W (η), η = α x + \int_{0}^{t} τ (t) d t

. Substituting this transformation into Eq. (5) gives the new nonlinear ODE:

(11)

(τ (t) - l (t)) W^{'} (η) + α^{4} χ_{1} (t) W^{″ ″} (η) = α^{2} χ_{2} (t) {(W^{3} (η) - W (η))}^{″},

wherein prime indicates differentiation with respect to the new parameter

η

. On the other hand, if Eq. (11) is integrated and the integral constant is ignored, the following equation is easily obtained

(12)

(τ (t) - l (t)) W (η) + α^{4} χ_{1} (t) W^{″'} (η) - α^{2} χ_{2} (t) (3 W^{2} (η) - 1) W^{'} (η) = 0 .

3.1. Implementation of the polynomial solutions

Consider Eq. (8) as a solution of Eq. (12). After balancing the highest order derivative term

W^{″'}

with the highest nonlinear term

W^{2} W^{'}

in (12), we get

n = k - 1

and the consistency condition states that

1 < k \leq 3

Type I When

ϱ = 1

and

k = 2

k = 3

Case 1. Solitary wave solution (when

k = 2

)

In this case, according to the relation

n = k - 1

n = 1

and the general solution of Eq. (12) takes the form

(13)

W (η) = a_{0} (t) + a_{1} (t) ϑ (η),

where

ϑ (η)

satisfies the auxiliary equation

(14)

ϑ^{'} (η) = b_{0} (t) + b_{1} (t) ϑ (η) + b_{2} (t) ϑ^{2} (η) .

Plugging Eqs. (13) and (14) into Eq. (12) and equating all coefficients of

ϑ^{ı} (η), ı = 0, 1, 2

, we get a system of algebraic equations that can be solved as follow:

(15)

\begin{matrix} a_{0} (t) & = \frac{α b_{1} (t) \sqrt{χ_{1} (t)}}{\sqrt{2 χ_{2} (t)}}, a_{1} (t) = \frac{2 b_{2} (t)}{b_{1} (t)} a_{0} (t), \\ b_{0} (t) & = \frac{α^{2} b_{1}^{2} (t) χ_{1} (t) - 2 χ_{2} (t)}{4 α^{2} b_{2} (t) χ_{1} (t)}, τ (t) = α l (t), \end{matrix}

where

χ_{1} (t) χ_{2} (t) > 0

and

α \neq 1

. Thus, the solution of Eq. (5) takes the form:

(16)

ω_{1} (x, t) = W_{1} (η) = - \tanh (\frac{\sqrt{χ_{2} (t)}}{\sqrt{2 χ_{1} (t)}} \times (x + \int_{0}^{t} l (t) d t)) .

Fig. 1 depicts a special symmetric solitary wave with unique maximum value, which is symmetric about the origin. Further, this solutions approaches zero when

| t | \to \infty

. The geometrical structure of this solution represents a bright-dark wave solution.

View original graphic|Download|PPT slide

Fig.1 The solitary wave solution $ω_{1} (x, t)$ given by (16) in 3D and 2D plots for $χ_{1} (t) = 2 + \cosh (t)$ , $χ_{2} (t) = 5 - \sin (t), l (t) = 1 + \cos^{2} (t)$ .

Case 2. M-type wave solution (when

k = 3

)

In this case, according to the relation

n = k - 1

n = 2

and the general solution of Eq. (12) takes the form

(17)

W (η) = a_{0} (t) + a_{1} (t) ϑ (η) + a_{2} (t) ϑ^{2} (η),

where

ϑ (η)

satisfies the auxiliary equation

(18)

ϑ^{'} (η) = b_{0} (t) + b_{1} (t) ϑ (η) + b_{2} (t) ϑ^{2} (η) + b_{3} (t) ϑ^{3} (η) .

Plugging Eqs. (17) and (18) into Eq. (12)and equating all coefficients of

ϑ^{ı} (η), ı = 0, 1, 2, 3

, we get a system of algebraic equations that can be solved as follow:

(19)

\begin{matrix} a_{0} (t) & = - 1 + \frac{2 α b_{2}^{2} (t) \sqrt{2 χ_{1} (t)}}{9 b_{3} (t) \sqrt{χ_{2} (t)}}, \\ a_{1} (t) & = \frac{4 α b_{2} (t) \sqrt{2 χ_{1} (t)}}{3 \sqrt{χ_{2} (t)}}, a_{2} (t) = \frac{2 α b_{3} (t) \sqrt{2 χ_{1} (t)}}{\sqrt{χ_{2} (t)}}, \\ b_{0} (t) & = \frac{b_{2} (t)}{54 b_{3}^{3} (t)} (2 b_{2}^{2} (t) - \frac{9 b_{3} (t) \sqrt{2 χ_{2} (t)}}{α \sqrt{χ_{1} (t)}}), \\ b_{1} (t) & = \frac{b_{2}^{2} (t)}{3 b_{3} (t)} - \frac{\sqrt{χ_{2} (t)}}{α \sqrt{2 χ_{1} (t)}}, τ (t) = α l (t), \end{matrix}

where

χ_{1} (t) χ_{2} (t) > 0

. Thus, the solution of Eq. (5)takes the form:

(20)

\begin{matrix} ω_{2} (x, t) = W_{2} (η) \\ = - (\frac{\exp (\frac{\sqrt{2 χ_{2} (t)} \times (x + \int_{0}^{t} l (t) d t)}{\sqrt{χ_{1} (t)}}) + 2 α \sqrt{χ_{1} (t)}}{\exp (\frac{\sqrt{2 χ_{2} (t)} \times (x + \int_{0}^{t} l (t) d t)}{\sqrt{χ_{1} (t)}}) - 2 α \sqrt{χ_{1} (t)}}), α \neq 1 . \end{matrix}

Fig. 2 shows a periodic M-shaped wave solution which is created due to changing the sign of the coefficient related to the weak dispersion. The peak value at the upper side is smaller than the absolute value of the peak value at the lower side.

View original graphic|Download|PPT slide

Fig.2 The M-type wave solution $ω_{2} (x, t)$ given by (20) in 3D and 2D plots for $χ_{1} (t) = 4 + \cos (t)$ , $χ_{2} (t) = 2 - \sin (t), l (t) = \sin (t) + \cos (t), α = - 0.5$ .

Type II When

ϱ = 2

and

k = 2

Case 1. Elliptic wave solution

In this case, according to the relation

n = k - 1

n = 1

and the general solution of Eq. (12) takes the form

(21)

W (η) = a_{0} (t) + a_{1} (t) ϑ (η),

where

ϑ (η)

satisfies the auxiliary equation

(22)

\begin{matrix} ϑ^{'} (η) \\ = \sqrt{b_{0} (t) + b_{1} (t) ϑ (η) + b_{2} (t) ϑ^{2} (η) + b_{3} (t) ϑ^{3} (η) + b_{4} (t) ϑ^{4} (η)} . \end{matrix}

Without losing the generality, we take

b_{1} (t) = b_{3} (t) = 0

in Eq. (22).

Plugging Eqs. (21) and (22) into Eq. (12) and equating all coefficients of

ϑ^{ı} (η), ı = 0, 2, 4

and

\sqrt{b_{0} (t) + b_{2} (t) ϑ^{2} (η) + b_{4} (t) ϑ^{4} (η)}

, we get a system of algebraic equations that can be solved as follow:

(23)

\begin{matrix} a_{0} (t) = 0, a_{1} (t) = \frac{\sqrt{- 2 b_{4} (t)}}{\sqrt{b_{2} (t)}}, \\ χ_{2} (t) = - α^{2} b_{2} (t) χ_{1} (t), τ (t) = α l (t), \end{matrix}

where

b_{2} (t) > 0 and b_{4} (t) < 0

. Thus, the solution of Eq. (5) takes the form:

(24)

ω_{3} (x, t) = W_{3} (η) = \frac{\sqrt{- 2 b_{4} (t)}}{\sqrt{b_{2} (t)}} \times ϑ (η), α \neq 1,

where

ϑ (η)

satisfies Eq. (22).

We mention that Eq. (22) has a variety of possible solutions in Jacobi elliptic functions type according to the choices of the arbitrary functions

b_{j} (t), j = 0, 2, 4

. So, we take

b_{j} (t) = b_{j} = constant, j = 0, 2, 4

. From the classification existed in Zhang [49], we take

(25)

\begin{matrix} b_{0} (t) = 1 - μ^{2}, b_{2} (t) = 2 μ^{2} - 1, \\ b_{4} (t) = - μ^{2}, ϑ (η) = cn (η, μ^{2}), \end{matrix}

where

0 < μ < 1

is the modulus of the Jacobi elliptic function. When

μ \to 0

μ \to 1

, the Jacobi elliptic function

cn (η)

degenerates into

\cos (η)

sech (η)

, respectively.

Substituting Eq. (25) into Eq. (24), we get the final solution shape of Eq. (5) as follows

(26)

ω_{3} (x, t) = W_{3} (η) = \frac{\sqrt{2 μ^{2}}}{\sqrt{2 μ^{2} - 1}} \times cn (η, μ^{2}) .

Figs. 3 and 4 depict special kinds of elliptic waves namely conoidal and chirped wave solutions when the modulus of the Jacobi elliptic function

μ = 0.8

and

μ = 0.99

, respectively.

View original graphic|Download|PPT slide

Fig.3 The Elliptic wave solution $ω_{3} (x, t)$ given by (26) in 3D and 2D plots for $l (t) = 1 + \cos^{2} (t), α = 0.5, μ = 0.8$ .

View original graphic|Download|PPT slide

Fig.4 The Elliptic wave solution $ω_{3} (x, t)$ given by (26) in 3D and 2D plots for $l (t) = 1 + \cos^{2} (t), α = 0.5, μ = 0.99$ .

Case 2. Periodic wave solution

Here, the solution has the same structure in Eq. (21) but with different auxiliary equation given by

(27)

ϑ^{'} (η) = ϑ (η) \sqrt{b_{0} (t) - b_{2} (t) ϑ^{2} (η)} .

Plugging Eqs. (21) and (27) into Eq. (12) and equating all coefficients of

ϑ^{ı} (η), ı = 0, 2

and

\sqrt{b_{0} (t) - b_{2} (t) ϑ^{2} (η)}

, we get a system of algebraic equations that can be solved as follow:

(28)

\begin{matrix} a_{0} (t) = 0, a_{1} (t) = \frac{α H (t) \sqrt{2 b_{2} (t)}}{\sqrt{χ_{2} (t)}}, \\ b_{0} (t) = \frac{χ_{2} (t)}{α^{2} H^{2} (t)}, χ_{1} (t) = - H^{2} (t), τ (t) = α l (t), \end{matrix}

where

b_{2} (t) χ_{2} (t) > 0

. Consequently, the solution of Eq. (5) takes the form:

(29)

\begin{matrix} ω_{4} (x, t) = W_{4} (η) \\ = \frac{2 α H (t) \sqrt{2 b_{2} (t) χ_{2} (t)} \times \exp (\frac{\sqrt{χ_{2} (t)}}{H (t)} (x + \int_{0}^{t} l (t) d t))}{1 + α^{2} H^{2} (t) b_{2} (t) χ_{2} (t) \times \exp (\frac{\sqrt{χ_{2} (t)}}{H (t)} (x + \int_{0}^{t} l (t) d t))}, \\ α \neq 1 . \end{matrix}

Fig. 5 shows a mixed breather-lump periodic wave solution with stable amplitude. This wave is symmetric about the origin and propagates parallel to the

t

-axis.

View original graphic|Download|PPT slide

Fig.5 The Periodic wave solution $ω_{4} (x, t)$ given by (29) in 3D and 2D plots for $H (t) = (2 + \cos (t))$ , $χ_{2} (t) = 5 - \sin (t), l (t) = \sin (t) + \cos (t), α = 0.5, b_{2} (t) = 1$ .

4. Conclusion

Herein, the main goal of this work is to exploit the unified method to attain new nonautonomous explicit and implicit wave solutions of the Cahn-Hilliard system when its coefficients varying with time in the area of mathematical physics, especially the field of energy and materials sciences. The obtained solutions are obtained in the polynomial type with different geometrical structures namely: bright-dark, M-type, conoidal soliton, chirped, and mixed breather-lump periodic wave solutions. The dynamical behaviors for these solutions in self-phase modulation medium are analyzed graphically through two-dimensional and three-dimensional graphics for different choices of the free parameters and arbitrary functions existed in the solutions. Our preferred method is capable of reducing the size of computational estimates and can be easily applied to a variety of physical challenges in the fields of theoretical physics and engineering. The data obtained demonstrate the effectiveness, simplicity and efficiency of the unified method.

Declaration of Competing Interest

Authors declare that they have no conflict of interest.

This research work is supported by Deanship of Scientific Research, Islamic University of Madinah (project Number: 442/2020). Many thanks to our colleagues in Deanship of Scientific Research, Islamic University of Madinah for their cooperation and complete support to achieve this work.

References

Publishing order | Descend order by publishing year | Descend order by cited within

[1]	H. Halidou, S. Abbagari, A. Houwe, M. Inc, B.B. Thomas. Phys. Lett. A, 430 (2022), p. 127951

[2]	S.W. Yao, L. Akinyemi, M. Mirzazadeh, M. Inc, K. Hosseini,M. Senol. Results Phys., 30 (2021), p. 104825

[3]	S.J. Chen, X. LÃ¼, X.F. Tang. Commun. Nonlinear Sci. Numer. Simul., 95 (2021), p. 105628

[4]	S. Kumar, R. Kumar, M.S. Osman, B. Samet. Numer. Methods Part. Differ. Equ.,37 (2) (2021), pp. 1250-1268 DOI: 10.1002/num.22577

[5]	A. Christlieb, J. Jones, K. Promislow, B. Wetton, M. Willoughby. J. Comput. Phys., 257 (2014), pp. 193-215

[6]	X. LÃ¼, Y.F. Hua, S.J. Chen, X.F. Tang. Commun. Nonlinear Sci. Numer. Simul., 95 (2021), p. 105612

[7]	X. LÃ¼, H.W. Hui, F.F. Liu,Y.L. Bai. Nonlinear Dyn., 106 (2) (2021), pp. 1491-1507 DOI: 10.1007/s11071-021-06524-x

[8]	C.A. Kennedy, I. Stewart, A. Facchini, I. Cersosimo, R. Mele, B. Chen, M. Uda, A. Kansal, A. Chiu, K.G. Kim, C. Dubeux. Proc. Natl. Acad. Sci., 112 (19) (2015), pp. 5985-5990 DOI: 10.1073/pnas.1504315112

[9]	X. LÃ¼, S.J. Chen. Commun. Nonlinear Sci. Numer. Simul., 103 (2021), p. 105939

[10]	M. Khater, A. Jhangeer, H. Rezazadeh, L. Akinyemi, M.A. Akbar, M. Inc,H. Ahmad. Opt. Quantum Electron., 53 (11) (2021), p. 609

[11]	F.S. Khodadad, S.M. Mirhosseini-Alizamini, B. GÃ¼nay, L. Akinyemi, H. Rezazadeh, M. Inc. Opt. Quantum Electron., 53 (12) (2021), p. 702

[12]	M.S. Osman, H. Almusawa, K.U. Tariq, S. Anwar, S. Kumar, M. Younis, W.X. Ma. J. Ocean Eng. Sci. (2021),

[13]	M.R. Fahim, P.R. Kundu, M.E. Islam, M.A. Akbar, M.S. Osman. J. Ocean Eng. Sci. (2021),

[14]	M.M. Khater, S. Muhammad, A. Al-Ghamdi,M. Higazy. J. Ocean Eng. Sci. (2022),

[15]	M.S. Osman, A. Korkmaz, H. Rezazadeh, M. Mirzazadeh, M. Eslami, Q. Zhou. Chin. J. Phys., 56 (5) (2018), pp. 2500-2506

[16]	M.S. Osman, A.M. Wazwaz. Appl. Math. Comput., 321 (2018), pp. 282-289

[17]	M. Alquran, M. Ali,O. Alshboul. J. Ocean Eng. Sci. (2022),

[18]	A. Yusuf, T.A. Sulaiman, A. Abdeljabbar,M. Alquran. J. Ocean Eng. Sci. (2021),

[19]	M. Wang, X. Li, J. Zhang. Phys. Lett. A, 372 (4) (2008), pp. 417-423

[20]	K.S. Nisar, K.K. Ali, M. Inc, M.S. Mehanna, H. Rezazadeh,L. Akinyemi. Results Phys., 33 (2022), p. 105153

[21]	K.S. Nisar, K.K. Ali, M. Inc, M.S. Mehanna, H. Rezazadeh,L. Akinyemi. Results Phys., 33 (2022), p. 105153

[22]	G. Yel, H.M. Baskonus,H. Bulut. Opt. Quantum Electron., 49 (9) (2017), p. 285

[23]	K.K. Ali, A.M. Wazwaz, M.S. Osman. Optik, 208 (2020), p. 164132

[24]	K. Hosseini,R. Ansari. Waves Random Complex Media, 27 (4) (2017), pp. 628-636 DOI: 10.1080/17455030.2017.1296983

[25]	A. Zafar, M. Shakeel, A. Ali, L. Akinyemi,H. Rezazadeh. Opt. Quantum Electron., 54 (1) (2022), p. 54 DOI: 10.9734/jpri/2022/v34i32a36108

[26]	K.U. Tariq, M. Inc, A. Pashrashid, M. Zubair,L. Akinyemi. J. Ocean Eng. Sci. (2022),

[27]	X. LÃ¼, S.J. Chen.Nonlinear Dyn., 103 (1) (2021), pp. 947-977 DOI: 10.1007/s11071-020-06068-6

[28]	Y.H. Yin, S.J. Chen, X. LÃ¼. Chin. Phys. B, 29 (12) ( 2020), p. 120502 DOI: 10.1088/1674-1056/aba9c4

[29]	X.J. He, X. LÃ¼, M.G. Li. Anal. Math. Phys., 11 (1) (2021), p. 4

[30]	S. Kumar, S. Malik, H. Rezazadeh, L. Akinyemi. Nonlinear Dyn. (2022),

[31]	J.G. Liu, W.H. Zhu, M.S. Osman, W.X. Ma. Eur. Phys. J. Plus, 135 (5) (2020), p. 412 DOI: 10.1080/10192557.2020.1867794

[32]	N.H. Sweilam, S.M. Ahmed,M. Adel. Math. Methods Appl. Sci. (2020),

[33]	L. Akinyemi, M. Senol b. E. Az-Zo, P. Veeresha, U. Akpan. Mod. Phys. Lett. B, 36 (01) (2022), p. 2150530

[34]	O.A. Arqub, M.S. Osman, A.H. Abdel-Aty, A.B. Mohamed,S. Momani. Mathematics, 8 (6) (2020), p. 923 DOI: 10.3390/math8060923

[35]	S.J. Chen, X. LÃ¼, M.G. Li, F. Wang. Phys. Scr.,96 (9) (2021), p. 095201 DOI: 10.1088/1402-4896/abf307

[36]	C.G. Zhu, R.H. Wang. Appl. Math. Comput., 208 (1) (2009), pp. 260-272

[37]	L. Akinyemi, M. Senol, M.S. Osman. J. Ocean Eng. Sci. (2021),

[38]	R.F. Zhang,S. Bilige. Nonlinear Dyn., 95 (4) (2019), pp. 3041-3048 DOI: 10.1007/s11071-018-04739-z

[39]	R.F. Zhang, M.C. Li,H.M. Yin. Nonlinear Dyn., 103 (1) (2021), pp. 1071-1079 DOI: 10.1007/s11071-020-06112-5

[40]	R.F. Zhang, M.C. Li, J.Y. Gan, Q. Li, Z.Z. Lan. Chaos,Solitons Fractals, 154 (2022), p. 111692

[41]	R.F. Zhang, M.C. Li. Nonlinear Dyn. (2022),

[42]	M. Fabrizio, F. Franchi, B. Lazzari, R. Nibbi. Phys. D, 378 (2018), pp. 46-53

[43]	P.O. Mchedlov-Petrosyan. Eur. J. Appl. Math., 27 (1) (2016), pp. 42-65

[44]	B. Inan, M.S. Osman, T. Ak,D. Baleanu. Math. Methods Appl. Sci., 43 (5) (2020), pp. 2588-2600 DOI: 10.1002/mma.6067

[45]	M.S. Osman, J.A. Machado,D. Baleanu. Opt. Quantum Electron., 50 (2) (2018), p. 73

[46]	H.I. Abdel-Gawad, M. Osman. J. Adv. Res., 6 (4) (2015), pp. 593-599

[47]	G. Hongjun, L. Changchun. Chaos, Solitons Fractals, 20 (2) (2004), pp. 253-258

[48]	M.B. Riaz, D. Baleanu, A. Jhangeer,N. Abbas. Results Phys., 25 (2021), p. 104151

[49]	L.H. Zhang. Appl. Math. Comput., 208 (1) (2009), pp. 144-155

Options

Abstract

Outlines

模态框（Modal）标题

Abstract

Cite this article

1. Introduction

2. A short note on the unified method

2.1. The polynomial type of wave solutions

2.2. The rational type of wave solutions

3. Solutions of Eq. (5) via the unified method

3.1. Implementation of the polynomial solutions

Fig.1 The solitary wave solution ω1(x,t) given by (16) in 3D and 2D plots for χ1(t)=2+cosh(t) , χ2(t)=5−sin(t),l(t)=1+cos2(t) .

Fig.2 The M-type wave solution ω2(x,t) given by (20) in 3D and 2D plots for χ1(t)=4+cos(t) , χ2(t)=2−sin(t),l(t)=sin(t)+cos(t),α=−0.5 .

Fig.3 The Elliptic wave solution ω3(x,t) given by (26) in 3D and 2D plots for l(t)=1+cos2(t),α=0.5,μ=0.8 .

Fig.4 The Elliptic wave solution ω3(x,t) given by (26) in 3D and 2D plots for l(t)=1+cos2(t),α=0.5,μ=0.99 .

Fig.5 The Periodic wave solution ω4(x,t) given by (29) in 3D and 2D plots for H(t)=(2+cos(t)) , χ2(t)=5−sin(t),l(t)=sin(t)+cos(t),α=0.5,b2(t)=1 .

4. Conclusion

References

Links

Fig.1 The solitary wave solution $ω_{1} (x, t)$ given by (16) in 3D and 2D plots for $χ_{1} (t) = 2 + \cosh (t)$ , $χ_{2} (t) = 5 - \sin (t), l (t) = 1 + \cos^{2} (t)$ .

Fig.2 The M-type wave solution $ω_{2} (x, t)$ given by (20) in 3D and 2D plots for $χ_{1} (t) = 4 + \cos (t)$ , $χ_{2} (t) = 2 - \sin (t), l (t) = \sin (t) + \cos (t), α = - 0.5$ .

Fig.3 The Elliptic wave solution $ω_{3} (x, t)$ given by (26) in 3D and 2D plots for $l (t) = 1 + \cos^{2} (t), α = 0.5, μ = 0.8$ .

Fig.4 The Elliptic wave solution $ω_{3} (x, t)$ given by (26) in 3D and 2D plots for $l (t) = 1 + \cos^{2} (t), α = 0.5, μ = 0.99$ .

Fig.5 The Periodic wave solution $ω_{4} (x, t)$ given by (29) in 3D and 2D plots for $H (t) = (2 + \cos (t))$ , $χ_{2} (t) = 5 - \sin (t), l (t) = \sin (t) + \cos (t), α = 0.5, b_{2} (t) = 1$ .