Manakov model of coupled NLS equation and its optical soliton solutions

Esra Unal Yilmaz; Farid Samsami Khodad; Yesim Saglam Ozkan; Reza Abazari; A.E. Abouelregal; Mayssam Tarighi Shaayesteh; Hadi Rezazadeh; Hijaz Ahmad

doi:10.1016/j.joes.2022.03.005

Journal of Ocean Engineering and Science >

2024 , Vol. 9 >Issue 4: 364 - 372

DOI: https://doi.org/10.1016/j.joes.2022.03.005

Original article

Manakov model of coupled NLS equation and its optical soliton solutions

Esra Unal Yilmaz ^a ,
Farid Samsami Khodad ^b ,
Yesim Saglam Ozkan ^c ,
Reza Abazari ^d ,
A.E. Abouelregal ,
Mayssam Tarighi Shaayesteh ^g ,
Hadi Rezazadeh ^b ,
Hijaz Ahmad ^,^h^,ⁱ

Expand

^a Department of Mathematics, Bolu Abant Izzet Baysal University, Bolu, Turkey
^b Faculty of Engineering Technology, Amol University of Special Modern Technologies, Amol, Iran
^c Department of Mathematics, Bursa Uludag University, Bursa, Turkey
^d Department of Mathematics and Applications, University of Mohaghegh Ardabili, Ardabil, Iran
^e Department of Mathematics, College of Science and Arts, Al-Qurayat, Jouf University, Saudi Arabia
^f Basic Sciences Research Unit, Jouf University, Saudi Arabia
^g Amir Kabir University, Tehran, Iran
^h Mathematics in Applied Sciences and Engineering Research Group, Scientific Research Center, Al-Ayen University, Nasiriyah 64001, Iraq
ⁱ Section of Mathematics, International Telematic University Uninettuno, Corso Vittorio Emanuele II, 39, Roma 00186, Italy

Received date: 2021-06-20

Revised date: 2022-03-07

Accepted date: 2022-03-07

Online published: 2022-03-17

Fold

Abstract

In the field of maritime transport, motion and energy, the dynamics of deep-sea waves is one of the major problems in ocean science. A mathematical modeling of dynamics of solitary waves in deep sea under the two-layer stratification leads to NLS equation, and consequently, the interaction two of them can be formulated by coupled NLS equation. In this work, extended auxiliary equation and the exp(âˆ’Ï-(Ï‡)) -expansion methods are employed to make the optical solutions of the Manakov model of coupled NLS equation. The methods used in this paper, in addition to providing the analysis of individual wave solutions, also provide general optical solutions. Some previously known solutions can be obtained by some special selections of parameters obtained by solving systems of algebraic equations. At this stage, it is more practical and convenient to apply methods with a symbolic calculation system.

Highlights

● Construction of optical soliton solutions Manakov model of coupled nonlinear Schrodinger equation.

● Applications of extended auxiliary equation methods.

● Hyperbolic, complex trigonometric, trigonometric and rational solutions.

● 3D, contour and 2D graphics for the solutions.

Key words： Manakov model; Extended auxiliary equation method; Optical solutions; Solitons

Cite this article

Esra Unal Yilmaz , Farid Samsami Khodad , Yesim Saglam Ozkan , Reza Abazari , A.E. Abouelregal , Mayssam Tarighi Shaayesteh , Hadi Rezazadeh , Hijaz Ahmad . Manakov model of coupled NLS equation and its optical soliton solutions[J]. Journal of Ocean Engineering and Science, 2024 , 9(4) : 364 -372 . DOI: 10.1016/j.joes.2022.03.005

1. Introduction

One of the main problems in oceanography is the study of inward waves dynamics [1] as a specific model of physical movements that occurs within fluids. The results of these studies are directly related to the issue of maritime transport, instantaneous motion and energy, as well as to the navy and engineering. The mathematical modeling of dynamics of inward waves in ocean leads to various forms of nonlinear evolution equations (NLEEs). Historically, the famous KdV equation was the first model developed by Korteweg and De Vries to explain the diffusion of low-amplitude inward waves in shallow water [2], [3]; however, this equation for long-amplitude inward waves will not be practical. To overcome this deficiency, especially for deep sea inward waves, Benjamin [4] and Ono [5] obtained Benjamin-Ono equation. In [6], Kubota et al. presented the intermediate long wave (ILW) equation for propagating weak nonlinear inward waves in stratified fluids of limited depth. In [7], Choi and Camassa obtained a form of equation that controls the evolution of inward waves at the interface between two immiscible inviscid fluids. However, in order to more accurately model the inner ocean waves in terms of two-layer stratification, [8] Song et al. proposed the Schrödinger nonlinear equation (NLSE), and as a result, the interaction of the two could be formulated by coupled NLSE. Therefore, finding accurate NLSE solutions and their coupled models will have a significant impact on the behavior of inward ocean waves and their interactions, respectively. It can be said that the solutions of these equations give more insight into the physical aspects of oceanic inward waves as well as the designated ocean science problems.

On the other hand, a great result that eliminates the divergence and propagation of radiative wave conduction is the nonlinear change in the refractive index of the medium, which is associated with the propagation of a strong electromagnetic wave. Due to the nonlinear change in the refractive index of the medium, it is possible to have wave packets in which the propagation of the wave occurs without any deformation in the wave envelop and are stationary in time [9]. Various people have worked on this type of phenomenon, such as Zakharov and Shabbat [10], who have proposed a theory for waves of the same polarity everywhere in two-dimensional geometry. The following two items can be considered as main features of their work:

a) A part of entered radiation to the medium is divided to a certain number of channels;

b) Each channel has a definite direction and their intensity decreases exponentially with increasing distance from its axis.

Manakov in [9] generalized the theory of proposed by Zhakharov and Shabat [10] to the case of waves of arbitrary polarization. He showed that when a wave with varying polarization enter into the nonlinear medium, it is separate into various beams with radiations of constant polarization. This case is known as polarization filter. An important result that Markov achieved in [9] relates to self-focused two-dimensional waves due to the one-dimensional self-modulation of the electromagnetic wave with arbitrary polarization. During the collision of latter waves, their velocities and amplitudes remained unchanged, but their polarizations do changed. Consequently, the mentioned electromagnetic waves can be considered as a soliton.

The mathematical modeling of the above statements phenomena was done by Manakov in [9] as an integrable coupled NLSE of Manakov type

(1)

\begin{matrix} i Ω_{t} + a_{1} Ω_{x x} + b_{1} {(| Ω |}^{2} + {| Π |}^{2}) Ω = 0, \\ i Π_{t} + a_{2} Π_{x x} + b_{2} {(| Π |}^{2} + {| Ω |}^{2}) Π = 0 . \end{matrix}

where

Π

and

Ω

are slowly varying envelops of the two interacting polarized waves and

a_{i}

and

b_{i}

i = 1, 2

are positive parameters. The term rogue or freak wave has long been used in marine science for waves that are much high and deeper than would be expected for the sea state [11]. Rogue waves detected only seconds before strike a ship, which can be seen in both shallow waters and oceans, are very dangerous [12]. These waves occur not only in the oceans [13], but also in the atmosphere [14], optics [15] and so on. The dynamics of rogue waves are well formulated by the NLSE. One of these models is the Manakov model of coupled NLS equation. Many studies have been done on rogue waves for this equation [16], [17], [18], [19].

Various effective approaches for obtaining exact solution of equations arising from modeling real-world problems have been successfully applied by scientists in recent years [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41], [42], [43], [44], [45], [46], [47], [48], [49], [50], [51], [52], [53]. These methods are also applied for finding the solitary wave solutions of system (1). Due to the balance between nonlinearity and dispersion, solitary wave solutions are stable localized waves that propagate without amplitude attenuation and deformation in a nonlinear environment [54], [55]. In the study [56], it was revealed that the peak of a solitary wave is weakly affected by the unsmooth boundary. The control of energy exchange of Manakov vector-soliton collision is studied in [57]. Radhakrishnan and Lakshmanan using the results of Painleve analysis obtained the bright and dark N-soliton solutions of the Manakov model (1) in [58]. In [59] Buryak et. al studied the interaction between dark and bright solitary wave solutions of model (1). In addition, by considering the analytical solution of the system (1), in [60], Balancer and Pare investigated some conditions for soliton switching and energy coupling in the case of equal cross- and self-phase modulation effects. Recently, in [61], [62], Yildirim applied the experimental equation method and the modified simple equation method, respectively, to obtain the soliton optical molecules of Manakov model (1).

In this paper, our first interest is applying the extended auxiliary equation (EAE) and

e x p (- ϖ (χ))

-expansion methods to emphasis its power in treatment nonlinear equations. These methods can be implemented on many of nonlinear models with various types of nonlinearity. The next interest is in the determination of solitary wave solutions of Manakov model (1) using present methods. These powerful and efficient methods have not been applied before to obtain the model solutions we study in this article.

2. Governing equation

In this section, we consider the Manakov model [18], [19], [57], [61], [62], [63]

(2)

\begin{matrix} i Ω_{t} + a_{1} Ω_{x x} + b_{1} {(| Ω |}^{2} + {| Π |}^{2}) Ω = 0, \\ i Π_{t} + a_{2} Π_{x x} + b_{2} {(| Π |}^{2} + {| Ω |}^{2}) Π = 0 . \end{matrix}

and studied soliton molecules or pulses with Manakov model [61], [62]. For this purpose, we use the following complex valued functions

(3)

Ω (x, t) = P_{1} (χ) e^{i φ (x, t)}, and Π (x, t) = P_{2} (χ) e^{i φ (x, t)},

with the wave transformation

(4)

χ = x - ρ t, and φ (x, t) = - k_{ι} x + w_{ι} t + ζ_{ι} .

where

φ (x, t), P_{ι} (χ)

are the phase and amplitude component functions,respectively. In the last equation, the parameter

k_{ι}

describes the soliton frequency,

w_{ι}

is its wave number while

ζ_{ι}

is the phase center. Substituting Eq. (3) into Eq. (2), for

ι = 1, 2

and

\tilde{ι} = 3 - ι

, the imaginary equation is as follows:

(5)

ρ = - 2 a_{ι} k_{ι},

and the real part is as follows:

(6)

a_{ι} \frac{d^{2}}{d χ^{2}} P_{ι} - (a_{ι} k_{ι}^{2} + w_{ι}) P_{ι} + b_{ι} P_{ι}^{3} + b_{ι} P_{ι} P_{\tilde{ι^{2}}} = 0,

With

P_{ι} = P_{\tilde{ι}}

, above equation is collapsed into

(7)

a_{ι} \frac{d^{2}}{d χ^{2}} P_{ι} - (a_{ι} k_{ι}^{2} + w_{ι}) P_{ι} + 2 b_{ι} P_{ι}^{3} = 0 .

By balancing

\frac{d^{2}}{d χ^{2}} P_{ι}

and

P_{ι}^{3}

, the balance number can be found.

3. Mathematical analysis of the Manakov model

The exact solutions of Eq. (2) are established by the help of the EAE method [64] and

e x p (- ϖ (χ))

-expansion method [66], [67], [68].

3.1. The solution of Eq. (1.1) using the EAE method

We will use the EAE method to solve Eq. (2). With the effect of balancing principle applied to Eq. (7), we have

(8)

\begin{matrix} u (χ) & = & n_{0} + n_{1} Π (χ) + n_{2} {(Π (χ))}^{2} \end{matrix}

Inserting Eq. (8) into Eq. (7) and equating all the coefficients of same power of

F^{i}

to zero, respectively, we have

(9)

\begin{matrix} 2 b_{ι} n_{2}^{3} + 8 a_{ι} n_{2} m_{6} = 0, \\ 3 a_{ι} n_{1} m_{6} + 6 b_{ι} n_{1} n_{2}^{2} = 0, \\ 6 b_{ι} n_{1}^{2} n_{2} + 6 b_{ι} n_{0} n_{2}^{2} + 6 a_{ι} n_{2} m_{4} = 0, \\ 2 a_{ι} n_{1} m_{4} + 12 b_{ι} n_{0} n_{1} n_{2} + 2 b_{ι} n_{1}^{3} = 0, \\ - a_{ι} k_{ι}^{2} n_{2} - w_{ι} n_{2} + 6 b_{ι} n_{0} n_{1}^{2} + 6 b_{ι} n_{0}^{2} n_{2} + 4 a_{ι} n_{2} m_{2} = 0, \\ a_{ι} n_{1} m_{2} - a_{ι} k_{ι}^{2} n_{1} - w_{ι} n_{1} + 6 b_{ι} n_{0}^{2} n_{1} = 0, \\ - w_{ι} n_{0} + 2 b_{ι} n_{0}^{3} - a_{ι} k_{ι}^{2} n_{0} + 2 a_{ι} n_{2} m_{0} = 0 . \end{matrix}

Above Eqs. (9) yield the following set of coefficients for the solutions.

(10)

\begin{matrix} m_{0} & = & \frac{n_{0} (w_{ι} - 2 b_{ι} n_{0}^{2} + a_{ι} k_{ι}^{2})}{2 a_{ι} n_{2}}, m_{2} = \frac{a_{ι} k_{ι}^{2} + w_{ι} - 6 b_{ι} n_{0}^{2}}{4 a_{ι}}, \\ m_{4} & = & - \frac{b_{ι} n_{0} n_{2}}{a_{ι}}, m_{6} = - \frac{b_{ι} n_{2}^{2}}{4 a_{ι}}, n_{0} = n_{0}, n_{1} = 0 . \end{matrix}

From (10) and (4), we obtain that Eq. (2) has the Jacobi elliptic function (JEF) solutions:

(11)

\begin{matrix} Ω (x, t) & = & n_{0} s n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{1}}{b_{1} n_{2}^{2}}} χ a_{1}^{- 1} m^{- 1}) \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(12)

\begin{matrix} Π (x, t) & = & n_{0} s n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{2}}{b_{2} n_{2}^{2}}} χ a_{2}^{- 1} m^{- 1}) \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

(13)

\begin{matrix} Ω (x, t) & = & {n_{0} m}^{- 1} {(s n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{1}}{b_{1} n_{2}^{2}}} χ a_{1}^{- 1} m^{- 1}))}^{- 1} \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(14)

\begin{matrix} Π (x, t) & = & {n_{0} m}^{- 1} {(s n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{2}}{b_{2} n_{2}^{2}}} χ a_{2}^{- 1} m^{- 1}))}^{- 1} \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

where

w_{ι} = - \frac{- m^{2} b_{ι} n_{0}^{2} + m^{2} a_{ι} {k_{ι}}^{2} - b_{ι} n_{0}^{2}}{m^{2}}

From (10) and (4), the JEF solutions are

(15)

\begin{matrix} Ω (x, t) & = & n_{0} m s n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{1}}{b_{1} n_{2}^{2}}} χ {a_{1}}^{- 1}) \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(16)

\begin{matrix} Π (x, t) & = & n_{0} m s n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{2}}{b_{2} n_{2}^{2}}} χ {a_{2}}^{- 1}) \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

(17)

\begin{matrix} Ω (x, t) & = & n_{0} {(s n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{1}}{b_{1} n_{2}^{2}}} χ {a_{1}}^{- 1}))}^{- 1} \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(18)

\begin{matrix} Π (x, t) & = & n_{0} {(s n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{2}}{b_{2} n_{2}^{2}}} χ {a_{2}}^{- 1}))}^{- 1} \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

where

w_{ι} = b_{ι} n_{0}^{2} - a_{ι} k_{ι}^{2} + b_{ι} {n_{0}}^{2} m^{2}

From (10) and (4) we conclude that Eq. (2) possess the JEF solutions:

(19)

\begin{matrix} Ω (x, t) & = & - n_{0} c n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{4} \sqrt{\frac{a_{1}}{b_{1} n_{2}^{2}}} χ {a_{1}}^{- 1} m^{- 1}) \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(20)

\begin{matrix} Π (x, t) & = & - n_{0} c n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{4} \sqrt{\frac{a_{2}}{b_{2} n_{2}^{2}}} χ {a_{2}}^{- 1} m^{- 1}) \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

(21)

\begin{matrix} Ω (x, t) & = & - n_{0} \frac{\sqrt{1 - m^{2}} s n (\frac{1}{2} b_{1} n_{0} n_{2} \sqrt{4} \sqrt{\frac{a_{1}}{b_{1} n_{2}^{2}}} χ a_{1}^{- 1} m^{- 1})}{d n (\frac{1}{2} b_{1} n_{0} n_{2} \sqrt{4} \sqrt{\frac{a_{1}}{b_{1} n_{2}^{2}}} χ a_{1}^{- 1} m^{- 1})} \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(22)

\begin{matrix} Π (x, t) & = & - n_{0} \frac{\sqrt{1 - m^{2}} s n (\frac{1}{2} b_{2} n_{0} n_{2} \sqrt{4} \sqrt{\frac{a_{2}}{b_{2} n_{2}^{2}}} χ a_{2}^{- 1} m^{- 1})}{d n (\frac{1}{2} b_{2} n_{0} n_{2} \sqrt{4} \sqrt{\frac{a_{2}}{b_{2} n_{2}^{2}}} χ a_{2}^{- 1} m^{- 1})} \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

where

w_{ι} = - \frac{- 2 m^{2} b_{ι} n_{0}^{2} + m^{2} a_{ι} k_{ι}^{2} + b_{ι} n_{0}^{2}}{m^{2}}

From (10) and (4), the solutions of Eq. (2) are

(23)

\begin{matrix} Ω (x, t) & = & - n_{0} d n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{1}}{b_{1} n_{2}^{2} (- 1 + m^{2})}} χ a_{1}^{- 1}) \\ \frac{1}{\sqrt{1 - m^{2}}} \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(24)

\begin{matrix} Π (x, t) & = & - n_{0} d n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{2}}{b_{2} n_{2}^{2} (- 1 + m^{2})}} χ a_{2}^{- 1}) \\ \frac{1}{\sqrt{1 - m^{2}}} \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

(25)

\begin{matrix} Ω (x, t) & = & - n_{0} {(d n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{1}}{b_{1} n_{2}^{2} (- 1 + m^{2})}} χ a_{1}^{- 1}))}^{- 1} \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(26)

\begin{matrix} Π (x, t) & = & - n_{0} {(d n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{2}}{b_{2} n_{2}^{2} (- 1 + m^{2})}} χ a_{2}^{- 1}))}^{- 1} \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

where

w_{ι} = - \frac{- b_{ι} n_{0}^{2} m^{2} + 2 b_{ι} n_{0}^{2} + a_{ι} k_{ι}^{2} m^{2} - a_{ι} k_{ι}^{2}}{m^{2} - 1}

From (10) and (4), the solutions are:

(27)

\begin{matrix} Ω (x, t) & = & - n_{0} {(c n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{1}}{b_{1} n_{2}^{2} (1 - m^{2})}} χ a_{1}^{- 1}))}^{- 1} \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(28)

\begin{matrix} Π (x, t) & = & - n_{0} {(c n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{2}}{b_{2} n_{2}^{2} (1 - m^{2})}} χ a_{2}^{- 1}))}^{- 1} \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

(29)

\begin{matrix} Ω (x, t) & = & n_{0} \frac{d n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{1}}{b_{1} n_{2}^{2} (1 - m^{2})}} χ a_{1}^{- 1})}{\sqrt{1 - m^{2}} s n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{1}}{b_{1} n_{2}^{2} (1 - m^{2})}} χ a_{1}^{- 1})} \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(30)

\begin{matrix} Π (x, t) & = & n_{0} \frac{d n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{2}}{b_{2} n_{2}^{2} (1 - m^{2})}} χ a_{2}^{- 1})}{\sqrt{1 - m^{2}} s n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{- 4 \frac{a_{2}}{b_{2} n_{2}^{2} (1 - m^{2})}} χ a_{2}^{- 1})} \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

where

w_{ι} = - \frac{- 2 b_{ι} n_{0}^{2} m^{2} + b_{ι} n_{0}^{2} + a_{ι} k_{ι}^{2} m^{2} - a_{ι} k_{ι}^{2}}{m^{2} - 1}

From (10) and (4), solutions of Eq. (2) are:

(31)

\begin{matrix} Ω (x, t) & = & - n_{0} d n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{4} \sqrt{\frac{a_{2}}{b_{ι} n_{2}^{2}}} χ a_{2}^{- 1}) \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(32)

\begin{matrix} Π (x, t) & = & - n_{0} d n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{4} \sqrt{\frac{a_{2}}{b_{ι} n_{2}^{2}}} χ a_{2}^{- 1}) \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

(33)

\begin{matrix} Ω (x, t) & = & - n_{0} \sqrt{1 - m^{2}} {(d n (\frac{b_{1} n_{0} n_{2}}{2} \sqrt{4} \sqrt{\frac{a_{2}}{b_{ι} n_{2}^{2}}} χ a_{2}^{- 1}))}^{- 1} \\ \exp (i (- k_{1} x + w_{1} t + ζ_{1})), \end{matrix}

(34)

\begin{matrix} Π (x, t) & = & - n_{0} \sqrt{1 - m^{2}} {(d n (\frac{b_{2} n_{0} n_{2}}{2} \sqrt{4} \sqrt{\frac{a_{2}}{b_{ι} n_{2}^{2}}} χ a_{2}^{- 1}))}^{- 1} \\ \exp (i (- k_{2} x + w_{2} t + ζ_{2})), \end{matrix}

where

w_{ι} = 2 b_{ι} n_{0}^{2} - a_{ι} k_{ι}^{2} - b_{ι} n_{0}^{2} m^{2}

3.2. The solution of Eq. (1.1) using the $e x p (- ϖ (χ))$ -expansion method

In this section, the

e x p (- ϖ (χ))

-expansion method is used to get the solutions of Eq. (2). Using homogeneous principle, balancing

u^{″}

and

u^{3}

, we have

3 m = m + 2

m = 1

. Therefore, the solution can be given as

(35)

u (χ) = n_{0} + n_{1} e x p (- w (χ)),

where

n_{1} \neq 0

n_{0}

is constant. By placing Eq. (35) and its derivatives in Eq. (7), and also by setting the different power factors of

e x p (- ϖ (χ))

equal to zero, we will have:

(36)

\begin{matrix} 2 a_{ι} n_{1} + 2 b_{ι} {n_{1}}^{3} & = & 0, \\ - a_{ι} {k_{ι}}^{2} n_{0} + a_{ι} n_{1} μ λ - w_{ι} n_{0} + 2 b_{ι} {n_{0}}^{3} & = & 0, \\ - a_{ι} {k_{ι}}^{2} n_{1} + 2 a_{ι} n_{1} μ + a_{ι} n_{1} λ^{2} + 6 b_{ι} {n_{0}}^{2} n_{1} - w_{ι} n_{1} & = & 0, \\ 3 a_{ι} n_{1} λ + 6 b_{ι} n_{0} {n_{1}}^{2} & = & 0 . \end{matrix}

The algebraic equations system gives the following set of coefficients for the solutions:

(37)

\begin{matrix} n_{0} & = & \frac{1}{2} n_{1} λ, n_{1} = n_{1}, a_{ι} = a_{ι}, b_{ι} = - \frac{a_{ι}}{n_{1}^{2}}, k_{ι} = k_{ι}, \\ μ & = & μ, w_{ι} = - \frac{1}{2} a_{ι} (2 k_{ι}^{2} + λ^{2} - 4 μ), λ = λ . \end{matrix}

From (37) and (4), the solution is obtained as follows:

(38)

\begin{matrix} Ω (x, t) = & \frac{(\frac{1}{2} n_{1} λ^{2} + \frac{1}{2} λ n_{1} \sqrt{λ^{2} - 4 μ} \tanh (\frac{1}{2} (x + 2 a_{1} k_{1} t) \sqrt{λ^{2} - 4 μ}) - 2 n_{1} μ)}{λ + \tanh (\frac{1}{2} \sqrt{λ^{2} - 4 μ} (x + 2 a_{1} k_{1} t)) \sqrt{λ^{2} - 4 μ}} \\ \times e^{i (- k_{1} x - \frac{1}{2} a_{1} (λ^{2} + 2 k_{1}^{2} - 4 μ) t + ζ_{1})} \end{matrix}

(39)

\begin{matrix} Π (x, t) = & \frac{(\frac{1}{2} n_{1} λ^{2} + \frac{1}{2} λ n_{1} \sqrt{λ^{2} - 4 μ} \tanh (\frac{1}{2} \sqrt{λ^{2} - 4 μ} (x + 2 a_{2} k_{2} t)) - 2 n_{1} μ)}{λ + \tanh (\frac{1}{2} \sqrt{λ^{2} - 4 μ} (x + 2 a_{2} k_{2} t)) \sqrt{λ^{2} - 4 μ}} \\ \times e^{i (- k_{2} x - \frac{1}{2} a_{2} (λ^{2} + 2 k_{2}^{2} - 4 μ) t + ζ_{2})} \end{matrix}

From (37) and (4), we obtain

(40)

\begin{matrix} Ω (x, t) = & \frac{(- \frac{1}{2} n_{1} λ^{2} + \frac{1}{2} n_{1} λ \sqrt{- λ^{2} + 4 μ} \tan (\frac{1}{2} \sqrt{- λ^{2} + 4 μ} (x + 2 a_{1} k_{1} t)) + 2 n_{1} μ)}{- λ + \tan (\frac{1}{2} \sqrt{- λ^{2} + 4 μ} (x + 2 a_{1} k_{1} t)) \sqrt{- λ^{2} + 4 μ}} \\ \times e^{i (- k_{1} x - \frac{1}{2} a_{1} (λ^{2} + 2 k_{1}^{2} - 4 μ) t + ζ_{1})} \end{matrix}

(41)

\begin{matrix} Π (x, t) = & \frac{(- \frac{1}{2} n_{1} λ^{2} + \frac{1}{2} λ n_{1} \sqrt{- λ^{2} + 4 μ} \tan (\frac{1}{2} (x + 2 a_{2} k_{2} t) \sqrt{- λ^{2} + 4 μ}) + 2 n_{1} μ)}{- λ + \tan (\frac{1}{2} \sqrt{- λ^{2} + 4 μ} (x + 2 a_{2} k_{2} t)) \sqrt{- λ^{2} + 4 μ}} \\ \times e^{i (- k_{2} x - \frac{1}{2} a_{2} (λ^{2} + 2 k_{2}^{2} - 4 μ) t + ζ_{2})} \end{matrix}

From (37) and (4), we get,

(42)

Ω (x, t) = \frac{n_{1} λ}{λ (x + 2 a_{1} k_{1} t) + 2} e^{i (- k_{1} x - \frac{1}{2} a_{1} (λ^{2} + 2 k_{1}^{2} - 4 μ) t + ζ_{1})}

(43)

Π (x, t) = \frac{n_{1} λ}{λ (x + 2 a_{2} k_{2} t) + 2} e^{i (- k_{2} x - \frac{1}{2} a_{2} (λ^{2} + 2 k_{2}^{2} - 4 μ) t + ζ_{2})}

From (37) and (4), we get,

(44)

Ω (x, t) = \frac{(\frac{1}{2} n_{1} λ e^{λ (x + 2 a_{1} k_{1} t)} + \frac{1}{2} n_{1} λ)}{e^{λ (x + 2 a_{1} k_{1} t)} - 1} e^{i (- k_{1} x - \frac{1}{2} a_{1} (λ^{2} + 2 k_{1}^{2} - 4 μ) t + ζ_{1})}

(45)

Π (x, t) = \frac{(\frac{1}{2} n_{1} λ e^{λ (x + 2 a_{2} k_{2} t)} + \frac{1}{2} n_{1} λ)}{e^{λ (x + 2 a_{2} k_{2} t)} - 1} e^{i (- k_{2} x - \frac{1}{2} a_{2} (λ^{2} + 2 k_{2}^{2} - 4 μ) t + ζ_{2})}

From (37) and (4), the solutions are

(46)

Ω (x, t) = \frac{n_{1}}{x + 2 a_{1} k_{1} t} e^{i (- k_{1} x - a_{1} {k_{1}}^{2} t + ζ_{1})}

(47)

Π (x, t) = \frac{n_{1}}{x + 2 a_{2} k_{2} t} e^{i (- k_{2} x - a_{2} {k_{2}}^{2} t + ζ_{2})}

4. Graphical demonstration

To find exact solutions to the governing equations, we successfully used

e x p (- w (χ))

and the developed auxiliary equation methods. Our figures show 3D surface diagrams and 2D-contour graphics show the obtained solutions. In this study, a variety of traveling waves solutions, periodic-like solutions, soliton-like solution are obtained through the trigonometric and exponential solutions.

5. Conclusion

In this paper, we find the new solutions of the Jacobi elliptic equation and the exact solutions of Eq. (2). In the present article, using the EAE method and the

e x p (- ϖ (χ))

-expansion method, we have obtained. With the help of Maple, the methods applied in this paper provide a powerful mathematical tool for finding accurate general solutions to a large number of NLPDEs or NLSEs in mathematical physics. To obtain Manakov model optical solitons, experimental equations and simple modified equations have been applied in [61], [62]. 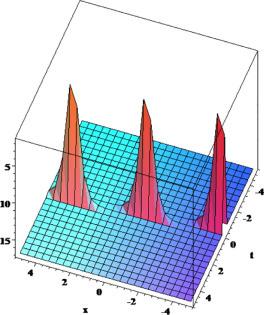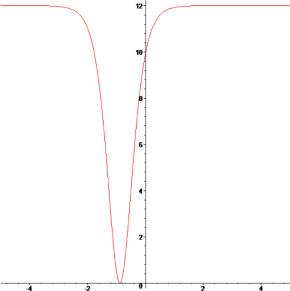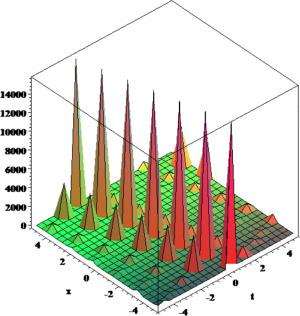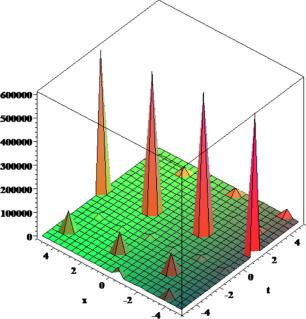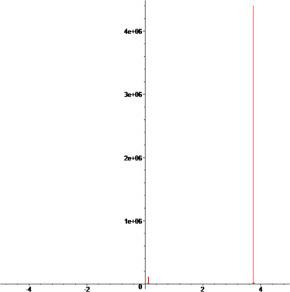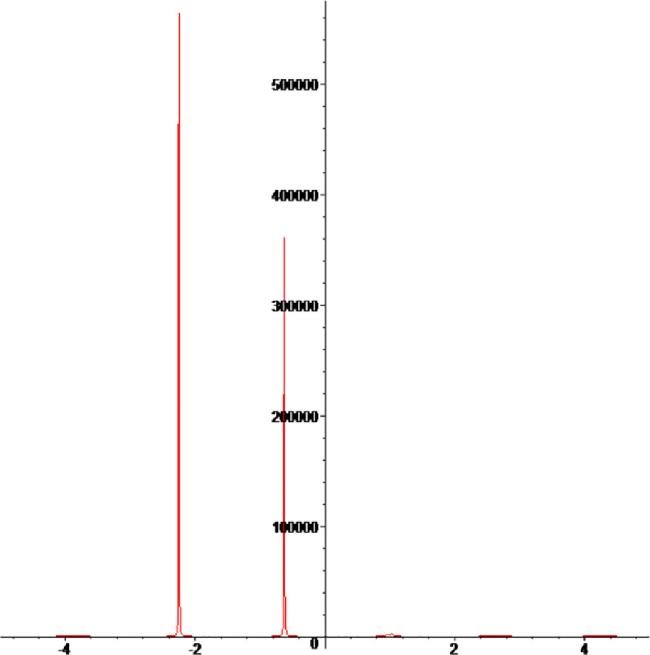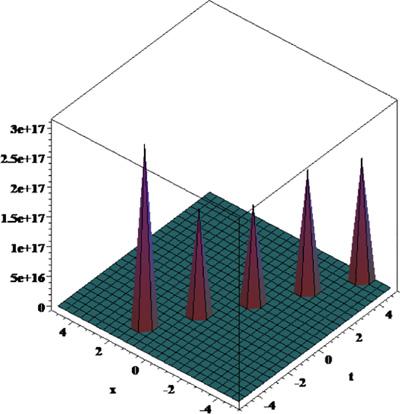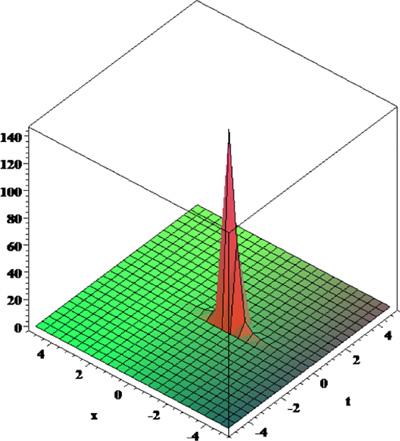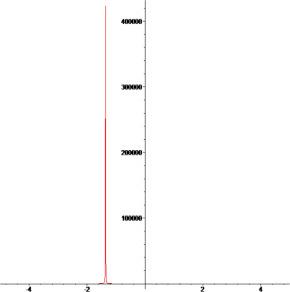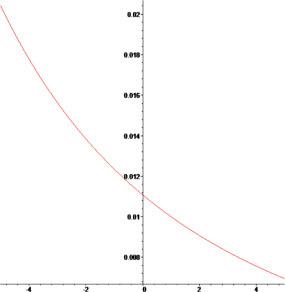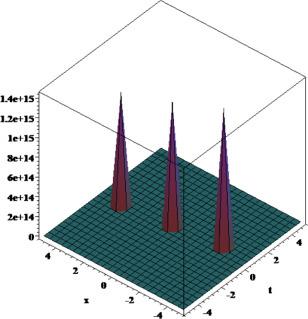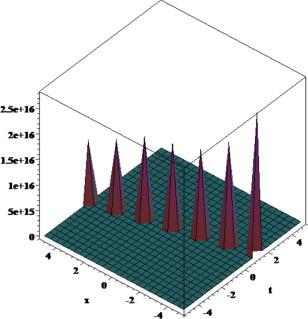The methods applied in this paper provide additional new solutions in addition to the solutions obtained by the experimental equation and the modified simple equation methods, and also, in theory, to accurately select the parameters, some of our solutions coincides with the solutions available in [61], [62]. Moreover, we plotted 3D and 2D plots for some of our obtained solutions for more dynamical properties. We get three forms of solitary wave solutions and Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 show that very obviously for these models. Fig. 5, Fig. 6, Fig. 13, Fig. 14 and 18 present multi-soliton solutions. Figs. 9 and 10 demonstrate rational function solutions. Fig. 17 shows single soliton solutions. As known, solitary waves and solitons are the specic types of localized solutions of several nonlinear physical models. By substituting the results within the original equation, we show that all solutions enrich the original equation. We wish this paper to contribute to future research and have different applications in the fields of modern optics and engineering.

View original graphic|Download|PPT slide

Fig.1 Profile of ${| Ω |}^{2}$ (38) for $n_{1} = 2$ , $k_{1} = 3, a_{1} = 0.2, ζ_{1} = 7, λ = 4, μ = 1$ , $y = z = 0 .$

View original graphic|Download|PPT slide

Fig.2 Profile of ${| Π |}^{2}$ (39) for $n_{1} = 2$ , $k_{2} = - 1, a_{2} = 5, ζ_{2} = 2, λ = 5, μ = 2$ , $y = z = 0 .$

View original graphic|Download|PPT slide

Fig.3 2D-profile of ${| Ω |}^{2}$ (38) for $t = 0.1$ , within $- 5 \leq x \leq 5 .$

View original graphic|Download|PPT slide

Fig.4 2D-profile of ${| Π |}^{2}$ (39) for $t = 0.1$ , within $- 5 \leq x \leq 5 .$

View original graphic|Download|PPT slide

Fig.5 Profile of ${| Ω |}^{2}$ (40) for $n_{1} = 1$ , $k_{1} = 4, a_{1} = 0.5, ζ_{1} = 3, μ = 4, λ = 2$ , $y = z = 0 .$

View original graphic|Download|PPT slide

Fig.6 Profile of ${| Π |}^{2}$ (41) for $n_{1} = 2$ , $k_{2} = 1, a_{2} = 4, ζ_{2} = 2, μ = 4, λ = 1$ , $y = z = 0 .$

View original graphic|Download|PPT slide

Fig.7 2D-profile of ${| Ω |}^{2}$ (40) for $t = 0.5$ , within $- 5 \leq x \leq 5 .$

View original graphic|Download|PPT slide

Fig.8 2D-profile of ${| Π |}^{2}$ (41) for $t = 0.5$ , within $- 5 \leq x \leq 5 .$

View original graphic|Download|PPT slide

Fig.9 Profile of ${| Ω |}^{2}$ (42) for $n_{1} = 2$ , $k_{1} = 3, a_{1} = 0.1, ζ_{1} = 5, λ = 2, μ = 1$ , $y = z = 0$ .

View original graphic|Download|PPT slide

Fig.10 Profile of ${| Π |}^{2}$ (43) for $n_{1} = 2$ , $k_{2} = 5, a_{2} = 3, ζ_{2} = 5, λ = 2, μ = 1$ , $y = z = 0 .$

View original graphic|Download|PPT slide

Fig.11 2D-profile of ${| Ω |}^{2}$ (42) for $t = 0.6$ , within $- 5 \leq x \leq 5$ .

View original graphic|Download|PPT slide

Fig.12 2D-profile of ${| Π |}^{2}$ (43) for $t = 0.6$ , within $- 5 \leq x \leq 5$ .

View original graphic|Download|PPT slide

Fig.13 Profile of ${| Ω |}^{2}$ (44) for $n_{1} = 1$ , $k_{1} = 5, a_{1} = 0.8, ζ_{1} = 1, λ = 5, μ = 0$ , $y = z = 0 .$

View original graphic|Download|PPT slide

Fig.14 Profile of ${| Π |}^{2}$ (45) for $n_{1} = 2$ , $k_{2} = 2, a_{2} = 1, ζ_{2} = 2, λ = 6, μ = 0$ , $y = z = 0 .$

View original graphic|Download|PPT slide

Fig.15 2D-profile of ${| Ω |}^{2}$ (44) for $t = 0.8$ , within $- 5 \leq x \leq 5 .$

View original graphic|Download|PPT slide

Fig.16 2D-profile of ${| Π |}^{2}$ (45) for $t = 0.8$ , within $- 5 \leq x \leq 5 .$

View original graphic|Download|PPT slide

Fig.17 Profile of ${| Ω |}^{2}$ (46) for $n_{1} = - 1$ , $k_{1} = 5, a_{1} = 0.8, ζ_{1} = 3, λ = 0, μ = 0$ , $y = z = 0$ .

View original graphic|Download|PPT slide

Fig.18 Profile of ${| Π |}^{2}$ (47) for $n_{1} = 2$ , $k_{2} = 1, a_{2} = 5, ζ_{2} = 2, λ = 0, μ = 0$ , $y = z = 0$ .

View original graphic|Download|PPT slide

Fig.19 2D-profile of ${| Ω |}^{2}$ (46) for $t = 0.7$ , within $- 5 \leq x \leq 5$ .

View original graphic|Download|PPT slide

Fig.20 2D-profile of ${| Π |}^{2}$ (47) for $t = 0.7$ , within $- 5 \leq x \leq 5$ .

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Publishing order | Descend order by publishing year | Descend order by cited within

[1]	Z. Wang, Y.K. Zhu. Chinese Journal of Theoretical and Applied Mechanics, 51 (2019), pp. 1589-1604

[2]	D.J. Korteweg, G. De Vries. Philos. Mag.,39 (240) (1895), pp. 422-443 DOI: 10.1080/14786449508620739

[3]	P. Karunakar, S. Chakraverty. Journal of Ocean Engineering and Science, 4 (2019), pp. 113-121

[4]	B.T. Benjamin. J Fluid Mech, 29 (03) (1967), pp. 559-592

[5]	O. Hiroaki. J. Phys. Soc. Jpn., 39 (1975), pp. 1082-1091

[6]	T. Kubota, D. Ko, L. Dobbs.AIAA Journal of Hydronautics, 12 (1978), pp. 157-165 DOI: 10.2514/3.63127

[7]	W. Choi, R. Camassa. J Fluid Mech, 396 (1999), pp. 1-36

[8]	S.Y. Song, J. Wang, J.M. Meng, J.B. Wang, P.X. Hu. Acta Physica Sinica, 59 (02) (2010), pp. 1123-1129

[9]	S.V. Manakov. Sov. Phys. JETP, 38 (1974), pp. 248-253

[10]	V.F. Zakharov, A.B. Shabat. Soy. Phys.-JETP, 34 (1972), pp. 62-70

[11]	K. Dysthe, H.E. Krogstad, P. Muller. Annu. Rev. Fluid Mech., 40 (2008), pp. 287-310 DOI: 10.1146/annurev. fluid.40.111406.102203

[12]	N. Akhmediev, E. Pelinovsky. Eur. Phys. J. Special Topics, 185 (5) (2010)

[13]	J. Gemmrich, C. Garrett. Ocean Eng., 37 (2-3) (2010), pp. 262-267

[14]	L. Stenflo, P.K. Shukla. J. Plasma Phys., 75 (6) (2009), pp. 841-847

[15]	D.R. Solli, C. Ropers, P. Koonath,B. Jalali. Nature, 450 (2007), pp. 1054-1057 DOI: 10.1038/nature06402 7172

[16]	A. Degasperis, S. Lombardo,M. Sommacal. Fluids, 4 (1) (2019), p. 57 DOI: 10.3390/fluids4010057

[17]	K. Manikandan, M. Senthilvelan, R.A. Kraenkel.The European Physical Journal B, 89 (10) (2016), pp. 1-11 DOI: 10.5318/wjo.v6.i1.1

[18]	N.V. Priya, M. Senthilvelan, M. Lakshmanan. Phys. Rev. E, 88 (2) (2013), p. 022918

[19]	S. Chen,D. Mihalache. J. Phys. A: Math. Theor., 48 (21) ( 2015), p. 215202 DOI: 10.1088/1751-8113/48/21/215202

[20]	M.A. Abdou. Journal of Ocean Engineering and Science, 2 (4) (2017), pp. 288-292

[21]	R.M. El-Shiekh, M. Gaballah. Journal of Ocean Engineering and Science, 5 (2) (2020), pp. 180-185

[22]	S. Kumar, M. Niwas, M.S. Osman. Commun Theor Phys (2021)

[23]	M. Mirzazadeh, L. Akinyemi, M. Senol,K. Hosseini. Optik Volume, 241 (2021), p. 166318

[24]	M. Islam, M. Akbar, H. Ahmad. Opt. Quantum Electron., 54 (2) (2022), pp. 1-23

[25]	H. Ahmad, A.E. Abouelregal, M. Benhamed, M.F. Alotaibi, A. Jendoubi. Sci Rep, 12 (1) (2022), pp. 1-8

[26]	E. Az-Zo'bi, W. Al Zoubi, L. Akinyemi, M. Senol, I. Alsaraireh, M. Mamat. Opt. Quantum Electron., 53 (2021) Article number: 132

[27]	L. Akinyemi, M. Senol, O. Iyiola. Math Comput Simul, 182 (2021), pp. 211-233

[28]	L. Akinyemi, K. Hosseini, S. Salahshour.Optik (Stuttg), 242 (2021), p. 167120

[29]	B. Ghanbari. Math Methods Appl Sci (2021),

[30]	H. M. Srivastava, H. GUnerhan,B. Ghanbari. Math Methods Appl Sci, 42 (18) (2019), pp. 7210-7221 DOI: 10.1002/mma.5827

[31]	Y.S. Ã-zkan, E. YaÅŸar. Alexandria Engineering Journal, 59 (6) (2020), pp. 5285-5293

[32]	B. Ghanbari, K.S. Nisar, M. Aldhaifallah. Advances in Difference Equations, 2020 (1) (2020), pp. 1-25

[33]	I. Ahmad, H. Ahmad, M. Inc, H. Rezazadeh, M.A. Akbar, M.M. Khater, L. Akinyemi, A. Jhangeer. Journal of Ocean Engineering and Science (2021),

[34]	Z. Korpinar, M. Inc, M. Bayram, M.S. Hashemi.Optik (Stuttg), 206 (2020), p. 163332

[35]	M.S. Hashemi, M. Inc, M. Bayram. Rev. Mex. Fis., 65 (5) (2019), pp. 529-535 DOI: 10.31349/revmexfis.65.529

[36]	T.D. Leta, W. Liu, A. El Achab, H. Rezazadeh, A. Bekir.Qualitative Theory of Dynamical Systems, 20 (1) (2021), pp. 1-22 DOI: 10.1155/2021/2805068

[37]	H. Rezazadeh, M. Younis, M. Eslami, M. Bilal,U. Younas. Math Model Nat Phenom, 16 (2021), p. 38 DOI: 10.1051/mmnp/2021001

[38]	K. Hosseini, K. Sadri, M. Mirzazadeh, Y.M. Chu, A. Ahmadian, B.A. Pansera,S. Salahshour. Results Phys., 23 (2021), p. 104035

[39]	K. Hosseini, S. Salahshour, M. Mirzazadeh, A. Ahmadian, D. Baleanu, A. Khoshrang. The European Physical Journal Plus, 136 (2) (2021), pp. 1-9

[40]	M.T. Darvishi, M. Najafi, A.M. Wazwaz. Phys. Scr.,96 (6) (2021), p. 065213 DOI: 10.1088/1402-4896/abf269

[41]	M.T. Darvishi, M. Najafi, A.M. Wazwaz. Chaos, Solitons & Fractals, 150 (2021), p. 111187

[42]	M.T. Darvishi, S. Ahmadian, S.B. Arbabi,M. Najafi. Opt. Quantum Electron., 50 (1) (2018), p. 32

[43]	S. Javeed, K. Saleem Alimgeer, S. Nawaz, A. Waheed, M. Suleman, D. Baleanu, M. Atif.Symmetry (Basel), 12 (1) (2020), p. 176 DOI: 10.3390/sym12010176

[44]	J.-H. He, M. Galal, M.H. Moatimid, Zekry, Forced nonlinear oscillator in a fractal space. facta universitatis series: Mechanical engineering, 2022, doi:10.22190/FUME220118004H http://casopisi.junis.ni.ac.rs/index.php/FUMechEng/article/view/10464.

[45]	M. Bilal, A.R. Seadawy, M. Younis, S.T.R. Rizvi, K. El-Rashidy, S.F. Mahmoud.Results Phys., 23 (2021), p. 103959

[46]	N. Anjum, J.H. He, Q.T. Ain, D. Tian.Facta Universitatis Series: Mechanical Engineering, 19 (4) (2021), pp. 601-612 DOI: 10.22190/fume210112025a

[47]	M. Bilal, A.R. Seadawy, M. Younis, S.T.R. Rizvi,H. Zahed. Math Methods Appl Sci, 44 (5) (2021), pp. 4094-4104 DOI: 10.1002/mma.7013

[48]	J.-H. He, Y.O. El-Dib.Facta Universitatis Series: Mechanical Engineering, 19 (4) (2021), pp. 735-750 DOI: 10.22190/fume210125033h

[49]	S. Sahoo, S. Saha Ray, M.A.M. Abdou, M. Inc, Y.M. Chu.Symmetry (Basel), 12 (6) (2020), p. 1001 DOI: 10.3390/sym12061001

[50]	H. Ahmad, T.A. Khan, H. Durur, G.M. Ismail, A. Yokus. Journal of Ocean Engineering and Science (2020),

[51]	S. Kumar, B. Mohan. Phys. Scr.,96 (12) (2021), p. 125255 DOI: 10.1088/1402-4896/ac3879

[52]	S.K. Dhiman, S. Kumar, H. Kharbanda. Mod. Phys. Lett. B (2021), p. 2150528

[53]	S. Kumar, S. Rani. Phys. Scr.,96 (12) (2021), p. 125202 DOI: 10.1088/1402-4896/ac1990

[54]	D.Y. Liu, B. Tian, Y. Jiang, X.Y. Xie, X.Y. Wu. Computers Mathematics with Applications, 71 (10) (2016), pp. 2001-2007

[55]	J. Denschlag, J.E. Simsarian, D.L. Feder, C.W. Clark, L.A. Collins, J. Cubizolles, L. Deng, E.W. Hagley, K. Helmerson, W.P. Reinhardt, S.L. Rolston, B.I. Schneide, W.D. Phillips. Science, 287 (2000), pp. 97-101

[56]	J.H. He, N. Qie,C.H. He. Results Phys., 24 (2021), p. 104104

[57]	R. Radhakrishnan, P.T. Dinda,G. Millot. Physical Review E, 69 (4) (2004), p. 046607

[58]	R. Radhakrishnan, M. Lakshmanan, J. Hietarinta. Physical Review E, 56 (2) (1997), pp. 2213-2216

[59]	A.V. Buryak, Y.S. Kivshar, D.F. Parker. Phys. Lett. A, 215 (1-2) (1996), p. 57

[60]	P.A. BÃ©langer, C. ParÃ©. Phys Rev A., 41 (9) (1990), pp. 5254-5256

[61]	Y. Yildirim.Optik (Stuttg), 185 (2019), p. 114651

[62]	Y. Yildirim.Optik (Stuttg), 185 (2019), p. 118288

[63]	K. Steiglitz.Physical Review E, 63 (4) (2001), p. 046607

[64]	G.Q. Xu. In Abstract and Applied Analysis, 2014 ( 2014)

[66]	M.A. Abdelrahman, E.H. Zahran, M.M. Khater. Global Journal of Science Frontier Research, 14 (4) (2014)

[67]	K. Hosseini, A. Bekir,R. Ansari. Opt. Quantum Electron., 49 (4) (2017), p. 131

[68]	A.R. Seadawy, D. Lu, M.M. Khater. Journal of Ocean Engineering and Science, 2 (2) (2017), pp. 137-142

Options

Abstract

Outlines

模态框（Modal）标题

Abstract

Cite this article

1. Introduction

2. Governing equation

3. Mathematical analysis of the Manakov model

3.1. The solution of Eq. (1.1) using the EAE method

3.2. The solution of Eq. (1.1) using the exp(−ϖ(χ)) -expansion method

4. Graphical demonstration

5. Conclusion

Fig.1 Profile of |Ω|2 (38) for n1=2, k1=3,a1=0.2,ζ1=7,λ=4,μ=1, y=z=0.

Fig.2 Profile of |Π|2 (39) for n1=2, k2=−1,a2=5,ζ2=2,λ=5,μ=2, y=z=0.

Fig.3 2D-profile of |Ω|2 (38) for t=0.1, within −5≤x≤5.

Fig.4 2D-profile of |Π|2 (39) for t=0.1, within −5≤x≤5.

Fig.5 Profile of |Ω|2 (40) for n1=1, k1=4,a1=0.5,ζ1=3,μ=4,λ=2, y=z=0.

Fig.6 Profile of |Π|2 (41) for n1=2, k2=1,a2=4,ζ2=2,μ=4,λ=1, y=z=0.

Fig.7 2D-profile of |Ω|2 (40) for t=0.5, within−5≤x≤5.

Fig.8 2D-profile of |Π|2 (41) for t=0.5, within −5≤x≤5.

Fig.9 Profile of |Ω|2 (42) for n1=2, k1=3,a1=0.1,ζ1=5,λ=2,μ=1, y=z=0.

Fig.10 Profile of |Π|2 (43) for n1=2, k2=5,a2=3,ζ2=5,λ=2,μ=1, y=z=0.

Fig.11 2D-profile of |Ω|2 (42) for t=0.6, within−5≤x≤5 .

Fig.12 2D-profile of |Π|2 (43) for t=0.6, within −5≤x≤5 .

Fig.13 Profile of |Ω|2 (44) for n1=1, k1=5,a1=0.8,ζ1=1,λ=5,μ=0, y=z=0.

Fig.14 Profile of |Π|2 (45) for n1=2, k2=2,a2=1,ζ2=2,λ=6,μ=0, y=z=0.

Fig.15 2D-profile of |Ω|2 (44) for t=0.8, within−5≤x≤5.

Fig.16 2D-profile of |Π|2 (45) for t=0.8, within −5≤x≤5.

Fig.17 Profile of |Ω|2 (46) for n1=−1, k1=5,a1=0.8,ζ1=3,λ=0,μ=0, y=z=0 .

Fig.18 Profile of |Π|2 (47) for n1=2, k2=1,a2=5,ζ2=2,λ=0,μ=0, y=z=0 .

Fig.19 2D-profile of |Ω|2 (46) for t=0.7, within−5≤x≤5 .

Fig.20 2D-profile of |Π|2 (47) for t=0.7, within −5≤x≤5 .

References

Links

3.2. The solution of Eq. (1.1) using the $e x p (- ϖ (χ))$ -expansion method

Fig.1 Profile of ${| Ω |}^{2}$ (38) for $n_{1} = 2$ , $k_{1} = 3, a_{1} = 0.2, ζ_{1} = 7, λ = 4, μ = 1$ , $y = z = 0 .$

Fig.2 Profile of ${| Π |}^{2}$ (39) for $n_{1} = 2$ , $k_{2} = - 1, a_{2} = 5, ζ_{2} = 2, λ = 5, μ = 2$ , $y = z = 0 .$

Fig.3 2D-profile of ${| Ω |}^{2}$ (38) for $t = 0.1$ , within $- 5 \leq x \leq 5 .$

Fig.4 2D-profile of ${| Π |}^{2}$ (39) for $t = 0.1$ , within $- 5 \leq x \leq 5 .$

Fig.5 Profile of ${| Ω |}^{2}$ (40) for $n_{1} = 1$ , $k_{1} = 4, a_{1} = 0.5, ζ_{1} = 3, μ = 4, λ = 2$ , $y = z = 0 .$

Fig.6 Profile of ${| Π |}^{2}$ (41) for $n_{1} = 2$ , $k_{2} = 1, a_{2} = 4, ζ_{2} = 2, μ = 4, λ = 1$ , $y = z = 0 .$

Fig.7 2D-profile of ${| Ω |}^{2}$ (40) for $t = 0.5$ , within $- 5 \leq x \leq 5 .$

Fig.8 2D-profile of ${| Π |}^{2}$ (41) for $t = 0.5$ , within $- 5 \leq x \leq 5 .$

Fig.9 Profile of ${| Ω |}^{2}$ (42) for $n_{1} = 2$ , $k_{1} = 3, a_{1} = 0.1, ζ_{1} = 5, λ = 2, μ = 1$ , $y = z = 0$ .

Fig.10 Profile of ${| Π |}^{2}$ (43) for $n_{1} = 2$ , $k_{2} = 5, a_{2} = 3, ζ_{2} = 5, λ = 2, μ = 1$ , $y = z = 0 .$

Fig.11 2D-profile of ${| Ω |}^{2}$ (42) for $t = 0.6$ , within $- 5 \leq x \leq 5$ .

Fig.12 2D-profile of ${| Π |}^{2}$ (43) for $t = 0.6$ , within $- 5 \leq x \leq 5$ .

Fig.13 Profile of ${| Ω |}^{2}$ (44) for $n_{1} = 1$ , $k_{1} = 5, a_{1} = 0.8, ζ_{1} = 1, λ = 5, μ = 0$ , $y = z = 0 .$

Fig.14 Profile of ${| Π |}^{2}$ (45) for $n_{1} = 2$ , $k_{2} = 2, a_{2} = 1, ζ_{2} = 2, λ = 6, μ = 0$ , $y = z = 0 .$

Fig.15 2D-profile of ${| Ω |}^{2}$ (44) for $t = 0.8$ , within $- 5 \leq x \leq 5 .$

Fig.16 2D-profile of ${| Π |}^{2}$ (45) for $t = 0.8$ , within $- 5 \leq x \leq 5 .$

Fig.17 Profile of ${| Ω |}^{2}$ (46) for $n_{1} = - 1$ , $k_{1} = 5, a_{1} = 0.8, ζ_{1} = 3, λ = 0, μ = 0$ , $y = z = 0$ .

Fig.18 Profile of ${| Π |}^{2}$ (47) for $n_{1} = 2$ , $k_{2} = 1, a_{2} = 5, ζ_{2} = 2, λ = 0, μ = 0$ , $y = z = 0$ .

Fig.19 2D-profile of ${| Ω |}^{2}$ (46) for $t = 0.7$ , within $- 5 \leq x \leq 5$ .

Fig.20 2D-profile of ${| Π |}^{2}$ (47) for $t = 0.7$ , within $- 5 \leq x \leq 5$ .