1. Introduction
2. Lie symmetry analysis
3. Lie symmetry reductions and soliton solutions
3.1. Subalgebra ${{\mathbb{V}}_{1}}:=\frac{\partial }{\partial x}$
3.2. Subalgebra ${{\mathbb{V}}_{2}}:=\frac{\partial }{\partial t}$
3.3. Subalgebra ${{\mathbb{V}}_{1}}+a{{\mathbb{V}}_{2}}:=\frac{\partial }{\partial t}+a\frac{\partial }{\partial t}$
3.4. For ${{c}_{0}}$, ${{c}_{1}}=0$ and ${{b}_{0}}$, ${{b}_{1}}\ne 0$.
3.4.1. Subalgebra ${{\mathbb{N}}_{1}}:=\frac{1}{2}mx\frac{\partial }{\partial x}+t\frac{\partial }{\partial t}+u\frac{\partial }{\partial u}$
3.4.2. Subalgebra ${{\mathbb{N}}_{2}}:=\frac{\partial }{\partial t}$
3.4.3. Subalgebra ${{\mathbb{N}}_{2}}+\lambda {{\mathbb{N}}_{3}}:=\frac{\partial }{\partial t}+\lambda \frac{\partial }{\partial x}$
3.5. For ${{c}_{0}}=0$ and ${{b}_{0}}$, ${{b}_{1}}$, ${{c}_{1}}\ne 0$ in Eq. (1) with $p=m-1$.
3.5.1. Subalgebra ${{\mathbb{M}}_{2}}:=\frac{\partial }{\partial x}$
3.5.2. Subalgebra ${{\mathbb{M}}_{3}}:=-{{e}^{-\left( m-1 \right){{c}_{1}}t}}{{b}_{0}}\frac{\partial }{\partial x}+{{e}^{-\left( m-1 \right){{c}_{1}}t}}\frac{\partial }{\partial t}+{{c}_{1}}{{e}^{-\left( m-1 \right){{c}_{1}}t}}u\frac{\partial }{\partial u}$
3.6. For ${{c}_{0}}=0$, ${{c}_{1}}=0$, ${{b}_{1}}=0$ and ${{b}_{0}}\ne 0$ in Eq. (1).
3.6.1. Subalgebra ${{\mathbb{P}}_{2}}:=\frac{\partial }{\partial t}$
3.6.2. Subalgebra ${{\mathbb{P}}_{2}}+\lambda {{\mathbb{P}}_{3}}:=\frac{\partial }{\partial t}+\lambda \frac{\partial }{\partial x}$
4. A generalized riccati equation mapping method overview
5. Soliton solutions of NCDR (1) via the generalized riccati equation mapping method
6. The modified kudryashov method overview
7. Solutions of NCDR (1) via the modified kudryashov method
8. Graphical illustrations of the soliton solutions
Fig. 1. Different soliton profiles for the solution (18) with the choice of parameter (a) K0=0.00956,a=0.009 with the range space 2≤x≤3,−3≤t≤8, (b) K0=0.000988,a=0.0279 with the range space 2≤x≤3,−3≤t≤8, (c) K0=0.000679,a=0.021 with the range space 5≤x≤6,−6≤t≤6. |
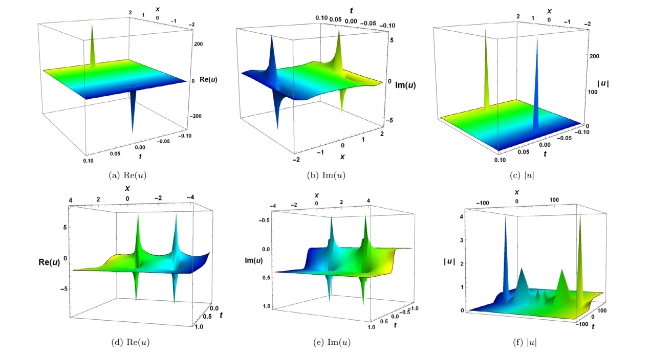
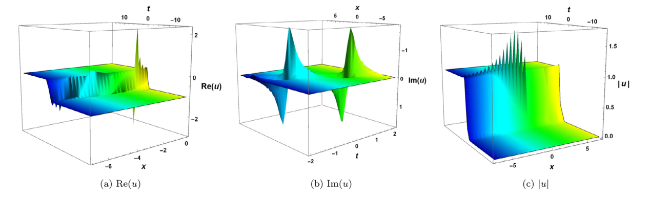
Fig. 2. Interaction of solitons with kink wave for the solution (40) with the choice of parameter (a)-(b)-(c) b0=−4i with the range space −2≤x≤2,−0.1≤t≤0.1, (d) b0=2i+1 with the range space −4≤x≤4,−0.3≤t≤1, (e) b0=7i with the range space −4≤x≤4,−1≤t≤1,(f) b0=2i+5 with the range space −150≤x≤150,−140≤t≤140. |
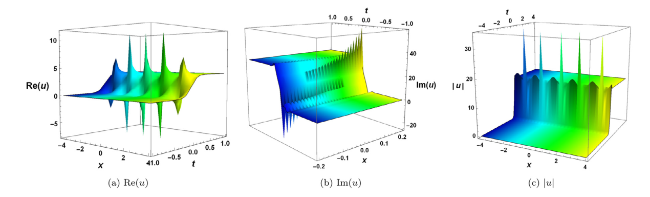
Fig. 3. Interaction of solitons with kink wave for the solution (41) with the choice of parameter (a) b0=−3i with the range space −4≤x≤4,−1≤t≤1, (b) b0=−8.03−4i with the range space −0.2≤x≤0.2,−1≤t≤1, (c) b0=−4i+4 with the range space −4≤x≤4,−5≤t≤4. |
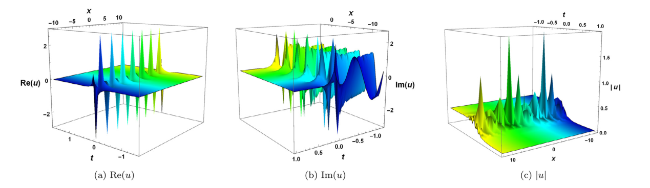
Fig. 4. Different soliton profiles for the solution (42) with the choice of parameter (a) b0=−6.2i with the range space −11≤x≤11,−1.5≤t≤1.7, (b) b0=−2i+3 with the range space −13≤x≤3,−1.2≤t≤1, (c) b0=−2i+13 with the range space −12≤x≤12,−1.2≤t≤1. |
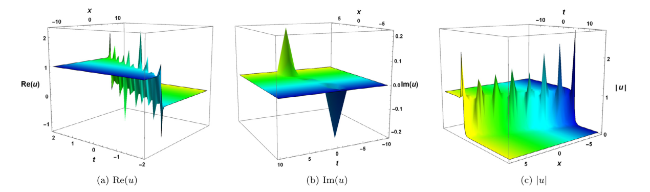
Fig. 5. Interaction of solitons with kink wave for the solution (74) with the choice of parameter (a) $\epsilon =-1$, ${{\lambda }_{3}}=2$, ${{\lambda }_{4}}=23$, ${{b}_{0}}=0.5$, ${{b}_{1}}=8.7$, $p=-1+7i$, ${{c}_{0}}=2$, ${{c}_{1}}=16$,G=0.0094,F=5.7 with the range space −10≤x≤10,−10≤t≤0.10, (b) $\epsilon =-1$, ${{\lambda }_{3}}=2$, ${{\lambda }_{4}}=23$, ${{b}_{0}}=0.5$, ${{b}_{1}}=9.7$, $p=-1+7i$, ${{c}_{0}}=2$, ${{c}_{1}}=16$,G=0.0094, F=5.7 with the range space −10≤x≤10,−10≤t≤0.10, (c) $\epsilon =-1$, ${{\lambda }_{3}}=2$, ${{\lambda }_{4}}=23$, ${{b}_{0}}=0.5$, ${{b}_{1}}=9.7$, $p=-1+7i$, ${{c}_{0}}=2$, ${{c}_{1}}=16$,G=0.0094,F=5.7 with the range space −10≤x≤10,−10≤t≤0.10. |
Fig. 6. Interaction of solitons with kink wave for the solution (79) with the choice of parameter (a) $\epsilon =-1$, ${{b}_{0}}=0.2$, ${{b}_{1}}=0.07$, $p=-1+7i$, ${{c}_{0}}=2$, ${{c}_{1}}=16$ with the range space −12≤x≤12,−2≤t≤2, (b) $\epsilon =-1$, ${{b}_{0}}=0.2$, ${{b}_{1}}=0.07$, $p=-1+7i$, ${{c}_{0}}=2$, ${{c}_{1}}=16$ with the range space −7≤x≤7,−10≤t≤10, (c) $\epsilon =-1$, ${{b}_{0}}=2$, ${{b}_{1}}=7$, $p=-1+i$, ${{c}_{0}}=2$, ${{c}_{1}}=16$ with the range space −7≤x≤7,−10≤t≤10. |
Fig. 7. Interaction of solitons with kink wave for the solution (94) with the choice of parameter (a) $\epsilon =-1$,b0=3,b1=0.2,p=−2+i,c0=2,c1=16,F=0.5,G=23 with the range space −7≤x≤0,−15≤t≤15, (b) $\epsilon =-1$,b0=3,b1=0.04,p=−2+i,c0=2,c1=16,F=20.05,G=0.03 with the range space −8≤x≤8,−2≤t≤2, (c) $\epsilon =-1$,b0=2,b1=7,p=−2+i,c0=2,c1=16,F=0.5,G=23 with the range space −7≤x≤7,−15≤t≤15. |
Fig. 8. Different Soliton profiles for the solution (95) with the choice of parameter (a) $\epsilon =-1$,b0=5,b1=5,p=−1+3i,c0=2,c1=6,F=0.05,G=0.03 with the range space −1≤x≤1,−2≤t≤2, (b) $\epsilon =-1$,b0=5,b1=5,p=−1+3i,c0=18,c1=6,F=0.05,G=0.03 with the range space −1≤x≤1,−2≤t≤2, (c) $\epsilon =-1$,b0=5,b1=5,p=−1+3i,c0=3.9,c1=6,F=2.05,G=0.03 with the range space −3≤x≤.3,−3≤t≤3. |