1. Introduction
2. Geometry modification expression method
2.1. Free-form deformation (FFD)
Fig. 1. The relationship between the global coordinate system and the lattice coordinate system. |
2.2. Geometry modification process of hull form
Table 1. Basic geometric parameters of the initial hull form model. |
| Geometric parameters | Scaled hull model |
|---|---|
| Length between perpendiculars | 7.279 m |
| Breadth | 0.703 m |
| Draft | 0.342 m |
| Wetted surface area | 9.438 m2 |
| Design speed | 2.196 m/s |
Fig. 2. Entire geometry modification process of the hull form. |
2.3. Various measures to prevent irrational hull models
Table 2. Two parameters used to prevent the appearance of irrational hulls. |
| Parameters | Actual values |
|---|---|
| τ | 2.0 |
| ψ | 0.8 |
3. Data collection
3.1. Hull performance acquisition method
3.2. The total resistance calculation theory
3.3. Design space of samples in the dataset
Table 3. The variation range of part of the deformation parameter. |
| Geometry modification parameter | Variable range |
|---|---|
| $α_{x}$ | [0.8,1.2] |
| $α_{y}$ | [0.8,1.2] |
| $α_{z}$ | [0.8,1.2] |
| $α_{d}$ | [−0.4,0] |
| $α_{f}$ | [0.7,1.3] |
Table 4. Parameters used to determine the lattice space. |
| Parameters | x-axis | y-axisn | z-axis |
|---|---|---|---|
| Offset rate | 0.05 | 0.05 | 0.05 |
| Rotation angle | 0.0 | 0.0 | 0.0 |
| N control points | 20 | 4 | 6 |
Fig. 3. Area division depends on different fixed directions. |
Table 5. Location of different areas and their fixed directions. |
| Boundary area | Area location | Fixed coordinate |
|---|---|---|
| Boundary-1 | x∈[−0.236,7.063] y∈[−0.572,0.063] z∈[−0.400,0.455] | X |
| Boundary-2 | x∈[−0.236,0.266] y∈[−0.572,0.063] z∈[−0.400,−0.105] | X,Z |
| Boundary-3 | x∈[7.0625,7.588] y∈[−0.572,0.063] z∈[−0.012,0.455] | X,Z |
Fig. 4. Area division depends on the movement range of the control points. |
Table 6. Location of different areas and the movement range of the control points in the area. |
| Area | Location | Direction | Scope |
|---|---|---|---|
| SABED | x∈[7.063,7.588] y∈[−0.572,0.063] z∈[−0.400,−0.012] | X | [−0.1,0.1] |
| SACQM | x∈[−0.236,7.588] y∈[−0.572,0.063] z∈[−0.400,0.455] | Y | [−0.1,0.1] |
| SABPM | x∈[−0.236,7.588] y∈[−0.572,0.063] z∈[−0.400,−0.012] | Y | [−0.2,0.2] |
| SKLQP | x∈[−0.236,0.266] y∈[−0.572,0.063] z∈[−0.105,0.455] | Y | [−0.3,0.3] |
| SABHG | x∈[6.477,7.588] y∈[−0.572,0.063] z∈[−0.400,−0.012] | Y | [−0.3,0.3] |
| SABED | x∈[7.063,7.588] y∈[−0.572,0.063] z∈[−0.400,−0.012] | Y | [−0.4,0.4] |
| SKLQP | x∈[−0.236,0.266] y∈[−0.572,0.063] z∈[−0.105,0.455] | Z | [−0.2,0.2] |
| SABHG | x∈[6.477,7.588] y∈[−0.572,0.063] z∈[−0.400,−0.012] | Z | [−0.2,0.2] |
| SABED | x∈[7.0625,7.58811] y∈[−0.572,0.063] z∈[−0.400,−0.012] | Z | [−0.3,0.3] |
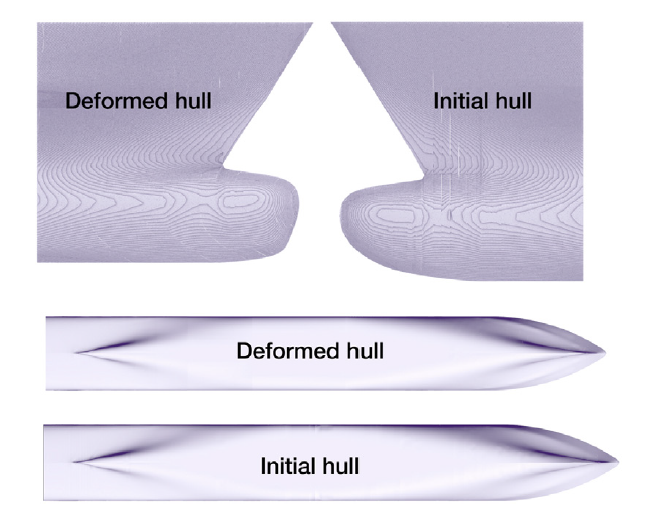
Fig. 5. Comparison of deformed hull model and initial hull model. |
3.4. Data collection
4. Construction and training of the deep learning model
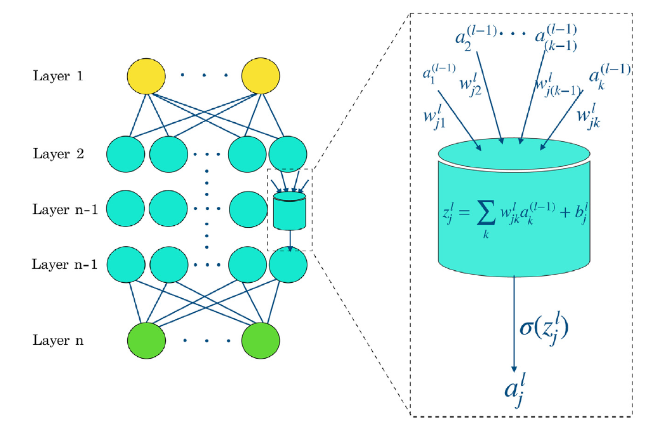
4.1. Fully connected neural network (FCNN)
Fig. 6. The schematic diagram of FCNN topology structure and single neuron processing. |
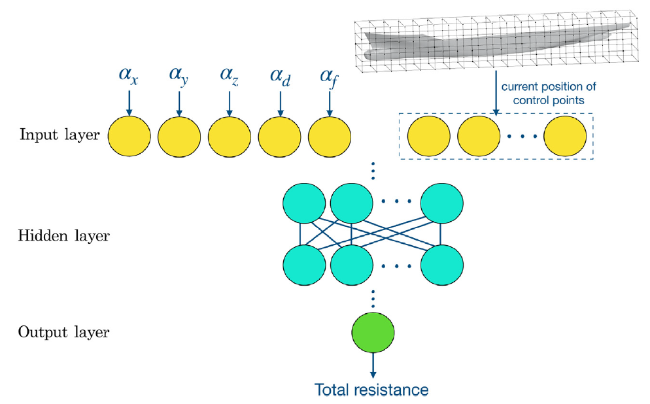
4.2. FCNN model construction
Fig. 7. Simplified schematic of the FCNN model. |
4.3. Hyperparameters tuning
Table 7. Default hyperparameters at the beginning of the tuning process. |
| Hyperparameters | Default value |
|---|---|
| L1 regularition rate | 0 |
| L2 regularition rate | 0 |
| Dropout rate | 0 |
| Batch size | 4096 |
Fig. 8. Loss vs. learning rate curve. |
Table 8. Parts of tuning result of hidden structure. |
| Hidden sturcture | % (%) | % (%) |
|---|---|---|
| (64) | 24.898 | 24.131 |
| (256, 4) | 15.386 | 12.712 |
| (32, 32) | 13.473 | 12.071 |
| (128, 4, 2) | 9.882 | 8.357 |
Fig. 9. (a) Training history for (64), (b) Training history for (256, 4), (c) Training history for (32, 32), and (d) Training history for (128, 4, 2). |
Table 9. Parts of tuning result of regularization parameters. |
| Empty Cell | L1 rate | L2 rate | dropout rate | % (%) | % (%) |
|---|---|---|---|---|---|
| case 1 | 0 | 0 | 0 | 26.167 | 194.706 |
| case 2 | 0.004 | 0.001 | 0.001 | 8.314 | 6.985 |
| case 3 | 0 | 0.128 | 0 | 6.512 | 5.752 |
| case 4 | 0.016 | 0 | 0.002 | 5.389 | 5.182 |
Fig. 10. (a) Training history for case 1, (b) Training history for case 2, (c) Training history for case 3, and (d) Training history for case 4. |
Table 10. Hyperparameters of the DL model at the beginning of the training process. |
| Hyperparameters | Value |
|---|---|
| Hidden sturcture | (256,4,2) |
| L1 regularition rate | 0.032 |
| L2 regularition rate | 0 |
| Dropout rate | 0 |
| Batch size | 4096 |
4.4. Training and testing
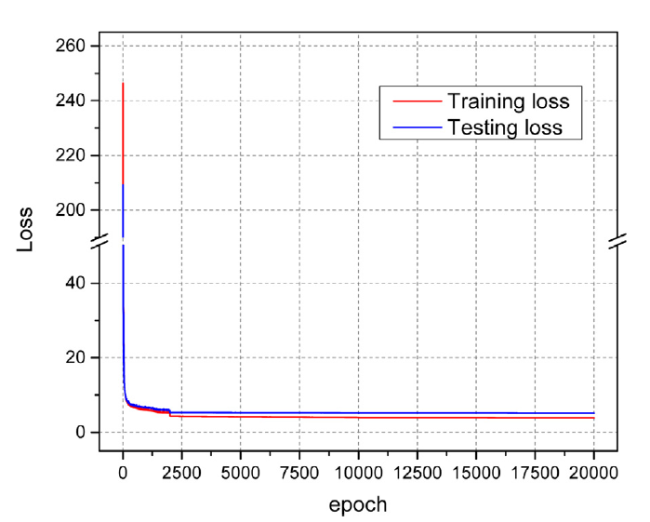
Fig. 11. The entire training history of the DL model. |
Fig. 12. (a) The training history from epoch 1 to epoch 3,000, and (b) The training history from epoch 3000 to epoch 20,000. |
Table 11. Training results of the final DL model. |
| Empty Cell | Loss | ||
|---|---|---|---|
| Training | 3.8844 | - | - |
| Testing | 5.1630 | 3.9754% | 4.7562% |
5. Model verification
Table 12. The details of the testing cases in step 1. |
| Testing case | Length rate | Breadth rate | Height rate | Draft rate | Froude number rate |
|---|---|---|---|---|---|
| Case 1 | (0.7, 1.3) | 1 | 1 | 0 | 1 |
| Case 2 | 1 | (0.7, 1.3) | 1 | 0 | 1 |
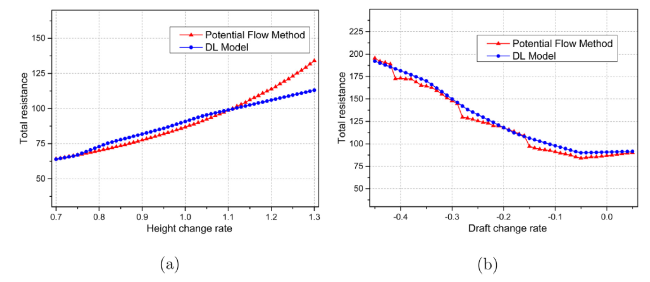
| Case 3 | 1 | 1 | (0.7, 1.3) | 0 | 1 |
| Case 4 | 1 | 1 | 1 | (−0.45, 0.05) | 1 |
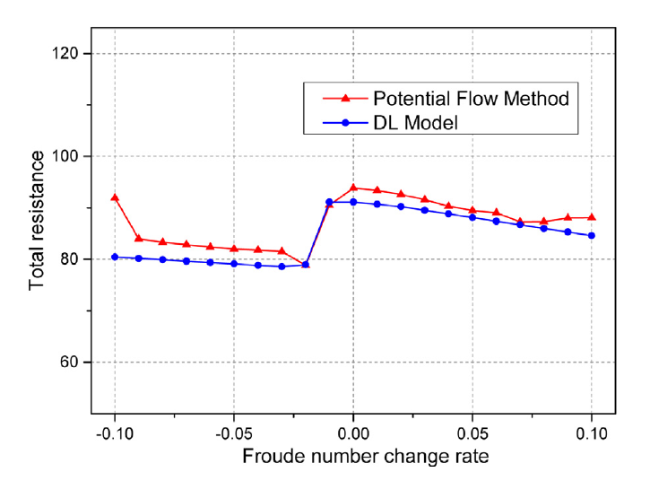
| Case 5 | 1 | 1 | 1 | 0 | (0.6, 1.4) |
Fig. 13. (a) Curve of total resistance vs. length change rate, and (b) Curve of total resistance vs. breadth change rate. |
Fig. 14. (a) Curve of total resistance vs. height change rate, and (b) Curve of total resistance vs. draft change rate. |
Fig. 15. Curve of total resistance vs. Froude number change rate. |
Fig. 16. Curve of total resistance of step 2. |
Table 13. The details of the testing cases in step 2. |
| Testing case | Length | Breadth | Height | Draft | Froude | ||
|---|---|---|---|---|---|---|---|
| Case 6 | 1 | 1 | 1 | 0 | 1 | (−0.1, 0.1) | 0.1 |
| Case 7 | 1 | 1 | 1 | 0 | (0.7, 1.3) | 0.1 | −0.07 |
| Case 9 | 1 | 1 | 1 | 0 | (0.7, 1.3) | −0.07 | 0.1 |
Fig. 17. (a) Curve of total resistance of Case 6, and (b) Curve of total resistance of Case 7. |
Table 14. Predicted errors in method verification. |
| Testing case | Max (entire) | Ave (entire) | Max (domain) | Ave (domain) |
|---|---|---|---|---|
| Case 1 | 27.85% | 6.90% | 7.90% | 4.08% |
| Case 2 | 13.93% | 5.44% | 10.85% | 4.92% |
| Case 3 | 15.64% | 4.92% | 6.95% | 4.25% |
| Case 4 | 9.62% | 4.22% | 9.62% | 4.63% |
| Case 5 | 33.87% | 8.35% | 19.12% | 5.67% |
| Case 6 | 12.50% | 3.09% | 12.50% | 3.09% |
| Case 7 | 14.37% | 4.68% | 14.37% | 4.68% |
| Case 8 | 15.70% | 4.48% | 15.70% | 4.48% |