1. Introduction
2. Mathematical construction
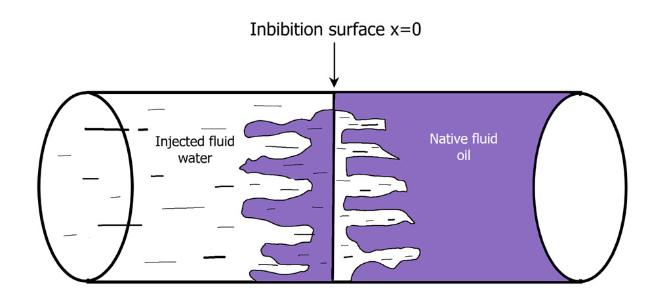
Fig.1 Natural mechanism of imbibition phenomenon. |
3. Analysis of RDTM
Table 1 Reduced differential transformation [19]. |
| Functional form | Transformed form |
|---|---|
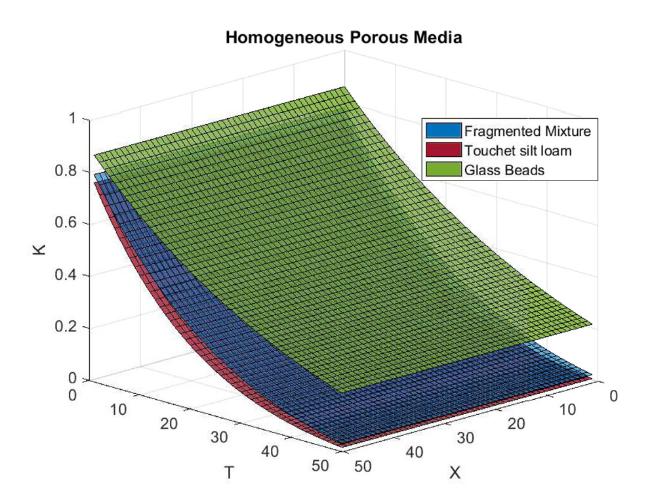
Fig.2 Water saturation in Fragmented mixture, Touchet silt loam and Glass beads for homogeneous porous media. |
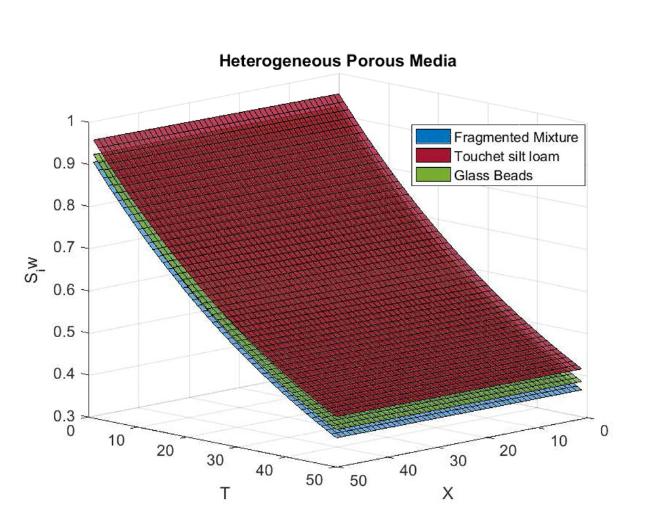
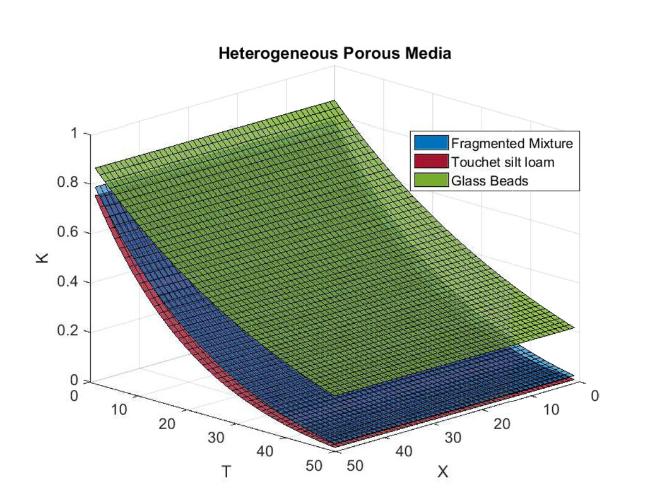
Fig.3 Water saturation in Fragmented mixture, Touchet silt loam and Glass beads for heterogeneous porous media. |
4. Mathematical solution
Table 2 Parametric value of parameters [23]. |
| Property | Fragmented mixture | Touchet silt loam | Glass beads |
|---|---|---|---|
| 2.89 | 1.82 | 7.3 | |
| 0.276 | 0.270 | 0.085 | |
| 17.2 | 75 | 29 | |
| 11.3 | 0.60 | 6.30 | |
| 0.443 | 0.485 | 0.370 |
5. Results and discussions
5.1. Effect of types of porous media on saturation profile for different porous materials
Table 3 Water saturation in Fragmented mixture in homogeneous porous media. |
| X T | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 | 0.007 | 0.008 | 0.009 | 0.01 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.905252 | 0.905668 | 0.906084 | 0.906501 | 0.906918 | 0.907336 | 0.907755 | 0.908174 | 0.908593 | 0.909014 |
| 0.2 | 0.819087 | 0.819444 | 0.819802 | 0.820160 | 0.820518 | 0.820877 | 0.821237 | 0.821597 | 0.821957 | 0.822318 |
| 0.3 | 0.741125 | 0.741433 | 0.741741 | 0.742049 | 0.742358 | 0.742667 | 0.742976 | 0.743286 | 0.743596 | 0.743907 |
| 0.4 | 0.670585 | 0.670851 | 0.671117 | 0.671383 | 0.671649 | 0.671916 | 0.672183 | 0.672451 | 0.672718 | 0.672986 |
| 0.5 | 0.606760 | 0.606990 | 0.607220 | 0.607451 | 0.607681 | 0.607912 | 0.608143 | 0.608375 | 0.608606 | 0.608838 |
| 0.6 | 0.549011 | 0.549210 | 0.549410 | 0.549610 | 0.549810 | 0.550010 | 0.550211 | 0.550412 | 0.550612 | 0.550813 |
| 0.7 | 0.496759 | 0.496932 | 0.497106 | 0.497280 | 0.497454 | 0.497628 | 0.497802 | 0.497977 | 0.498151 | 0.498326 |
| 0.8 | 0.449480 | 0.449632 | 0.449783 | 0.449935 | 0.450086 | 0.450238 | 0.450390 | 0.450542 | 0.450694 | 0.450847 |
| 0.9 | 0.406702 | 0.406834 | 0.406966 | 0.407099 | 0.407231 | 0.407364 | 0.407497 | 0.407630 | 0.407763 | 0.407896 |
| 1 | 0.367995 | 0.368111 | 0.368227 | 0.368343 | 0.368459 | 0.368575 | 0.368692 | 0.368808 | 0.368924 | 0.369041 |
Table 4 Water saturation in Fragmented mixture in heterogeneous porous media. |
| X T | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 | 0.007 | 0.008 | 0.009 | 0.01 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.905117 | 0.905397 | 0.905678 | 0.905958 | 0.906239 | 0.906521 | 0.906803 | 0.907085 | 0.907367 | 0.907650 |
| 0.2 | 0.818969 | 0.819208 | 0.819447 | 0.819686 | 0.819925 | 0.820165 | 0.820405 | 0.820645 | 0.820886 | 0.821127 |
| 0.3 | 0.741022 | 0.741226 | 0.741430 | 0.741634 | 0.741839 | 0.742043 | 0.742248 | 0.742453 | 0.742659 | 0.742864 |
| 0.4 | 0.670494 | 0.670669 | 0.670844 | 0.671019 | 0.671194 | 0.671369 | 0.671544 | 0.671720 | 0.671896 | 0.672072 |
| 0.5 | 0.606680 | 0.606830 | 0.606980 | 0.607130 | 0.607281 | 0.607431 | 0.607582 | 0.607732 | 0.607883 | 0.608034 |
| 0.6 | 0.548941 | 0.549070 | 0.549199 | 0.549328 | 0.549457 | 0.549587 | 0.549716 | 0.549846 | 0.549975 | 0.550105 |
| 0.7 | 0.496697 | 0.496808 | 0.496919 | 0.497031 | 0.497142 | 0.497254 | 0.497366 | 0.497477 | 0.497589 | 0.497701 |
| 0.8 | 0.449425 | 0.449521 | 0.449618 | 0.449714 | 0.449811 | 0.449907 | 0.450004 | 0.450100 | 0.450197 | 0.450294 |
| 0.9 | 0.406653 | 0.406737 | 0.406820 | 0.406904 | 0.406987 | 0.407071 | 0.407155 | 0.407238 | 0.407322 | 0.407406 |
| 1 | 0.367952 | 0.368025 | 0.368097 | 0.368170 | 0.368242 | 0.368315 | 0.368388 | 0.368461 | 0.368534 | 0.368606 |
Table 5 Water saturation rate in Touchet silt loam in homogeneous porous media. |
| X T | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 | 0.007 | 0.008 | 0.009 | 0.01 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.905605 | 0.906375 | 0.907147 | 0.907922 | 0.908700 | 0.909480 | 0.910262 | 0.911047 | 0.911835 | 0.912625 |
| 0.2 | 0.819374 | 0.820020 | 0.820667 | 0.821317 | 0.821968 | 0.822621 | 0.823277 | 0.823934 | 0.824593 | 0.825254 |
| 0.3 | 0.741359 | 0.741901 | 0.742445 | 0.742990 | 0.743537 | 0.744085 | 0.744635 | 0.745186 | 0.745739 | 0.746293 |
| 0.4 | 0.670775 | 0.671232 | 0.671690 | 0.672148 | 0.672608 | 0.673069 | 0.673531 | 0.673995 | 0.674459 | 0.674925 |
| 0.5 | 0.606915 | 0.607300 | 0.607686 | 0.608073 | 0.608460 | 0.608849 | 0.609238 | 0.609629 | 0.610020 | 0.610412 |
| 0.6 | 0.549136 | 0.549462 | 0.549788 | 0.550115 | 0.550443 | 0.550771 | 0.551100 | 0.551429 | 0.551759 | 0.552090 |
| 0.7 | 0.496861 | 0.497136 | 0.497413 | 0.497690 | 0.497967 | 0.498245 | 0.498523 | 0.498802 | 0.499082 | 0.499361 |
| 0.8 | 0.449563 | 0.449797 | 0.450032 | 0.450267 | 0.450502 | 0.450738 | 0.450974 | 0.451211 | 0.451448 | 0.451685 |
| 0.9 | 0.406769 | 0.406968 | 0.407168 | 0.407368 | 0.407568 | 0.407769 | 0.407970 | 0.408171 | 0.408373 | 0.408574 |
| 1 | 0.368049 | 0.368219 | 0.368390 | 0.368560 | 0.368731 | 0.368902 | 0.369074 | 0.369245 | 0.369417 | 0.369589 |
Table 6 Water saturation in Touchet silt loam in heterogeneous porous media. |
| X T | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 | 0.007 | 0.008 | 0.009 | 0.01 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.905375 | 0.905915 | 0.906455 | 0.906998 | 0.907541 | 0.908087 | 0.908634 | 0.909182 | 0.909732 | 0.910283 |
| 0.2 | 0.819179 | 0.819628 | 0.820079 | 0.820530 | 0.820983 | 0.821437 | 0.821892 | 0.822348 | 0.822806 | 0.823264 |
| 0.3 | 0.741192 | 0.741567 | 0.741943 | 0.742320 | 0.742697 | 0.743076 | 0.743455 | 0.743835 | 0.744216 | 0.744598 |
| 0.4 | 0.670633 | 0.670946 | 0.671260 | 0.671575 | 0.671890 | 0.672206 | 0.672523 | 0.672841 | 0.673159 | 0.673477 |
| 0.5 | 0.606793 | 0.607055 | 0.607318 | 0.607581 | 0.607845 | 0.608110 | 0.608375 | 0.608640 | 0.608906 | 0.609173 |
| 0.6 | 0.549031 | 0.549252 | 0.549472 | 0.549693 | 0.549914 | 0.550136 | 0.550358 | 0.550580 | 0.550803 | 0.551026 |
| 0.7 | 0.496770 | 0.496955 | 0.497140 | 0.497326 | 0.497512 | 0.497698 | 0.497884 | 0.498071 | 0.498258 | 0.498446 |
| 0.8 | 0.449485 | 0.449640 | 0.449796 | 0.449953 | 0.450109 | 0.450266 | 0.450423 | 0.450580 | 0.450737 | 0.450895 |
| 0.9 | 0.406701 | 0.406832 | 0.406964 | 0.407096 | 0.407228 | 0.407360 | 0.407492 | 0.407625 | 0.407758 | 0.407891 |
| 1 | 0.367990 | 0.368102 | 0.368213 | 0.368324 | 0.368436 | 0.368548 | 0.368660 | 0.368772 | 0.368884 | 0.368996 |
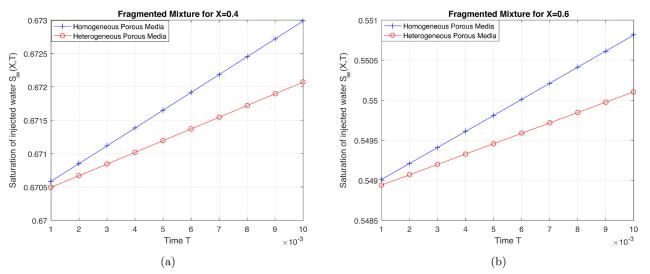
Fig.4 Water saturation vs. time in Fragmented mixture for fixed distance (a) (b) . |
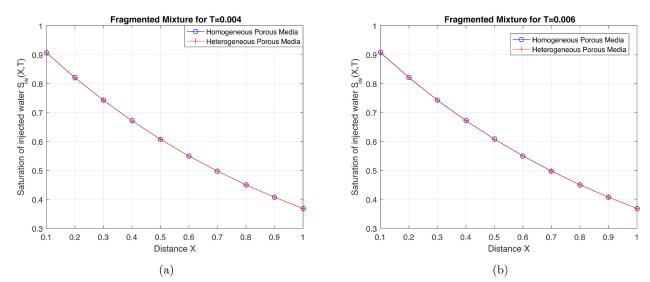
Fig.5 Water saturation vs. distance in Fragmented mixture for fixed time (a) (b) . |
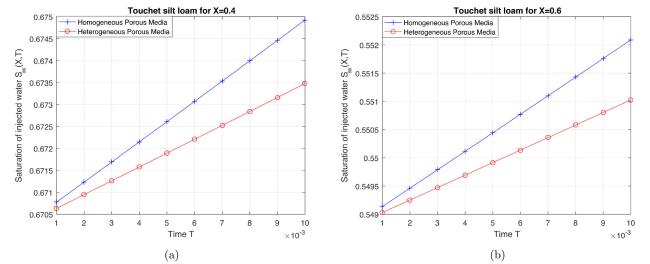
Fig.6 Water saturation vs. time in Touchet silt loam for fixed distance (a) (b) . |
Table 7 Water saturation in Glass beads in homogeneous porous media. |
| X T | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 | 0.007 | 0.008 | 0.009 | 0.01 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.904975 | 0.905113 | 0.905251 | 0.905389 | 0.905528 | 0.905666 | 0.905804 | 0.905942 | 0.906080 | 0.906219 |
| 0.2 | 0.818853 | 0.818975 | 0.819097 | 0.819219 | 0.819342 | 0.819464 | 0.819586 | 0.819709 | 0.819831 | 0.819954 |
| 0.3 | 0.740927 | 0.741035 | 0.741143 | 0.741252 | 0.741360 | 0.741469 | 0.741577 | 0.741686 | 0.741794 | 0.741903 |
| 0.4 | 0.670416 | 0.670513 | 0.670609 | 0.670705 | 0.670801 | 0.670898 | 0.670994 | 0.671090 | 0.671187 | 0.671283 |
| 0.5 | 0.606616 | 0.606702 | 0.606787 | 0.606873 | 0.606959 | 0.607044 | 0.607130 | 0.607216 | 0.607302 | 0.607387 |
| 0.6 | 0.548888 | 0.548964 | 0.549040 | 0.549117 | 0.549193 | 0.549269 | 0.549346 | 0.549422 | 0.549498 | 0.549575 |
| 0.7 | 0.496653 | 0.496721 | 0.496789 | 0.496857 | 0.496925 | 0.496994 | 0.497062 | 0.497130 | 0.497198 | 0.497266 |
| 0.8 | 0.449390 | 0.449450 | 0.449511 | 0.449572 | 0.449633 | 0.449693 | 0.449754 | 0.449815 | 0.449876 | 0.449937 |
| 0.9 | 0.406624 | 0.406678 | 0.406733 | 0.406787 | 0.406841 | 0.406896 | 0.406950 | 0.407004 | 0.407059 | 0.407113 |
| 1 | 0.367928 | 0.367977 | 0.368025 | 0.368074 | 0.368122 | 0.368171 | 0.368220 | 0.368268 | 0.368317 | 0.368366 |
Table 8 Water saturation in Glass beads in heterogeneous porous media . |
| X T | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 | 0.007 | 0.008 | 0.009 | 0.01 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.904930 | 0.905023 | 0.905115 | 0.905208 | 0.905301 | 0.905394 | 0.905486 | 0.905579 | 0.905672 | 0.905765 |
| 0.2 | 0.818812 | 0.818894 | 0.818976 | 0.819057 | 0.819139 | 0.819221 | 0.819303 | 0.819385 | 0.819466 | 0.819548 |
| 0.3 | 0.740890 | 0.740962 | 0.741035 | 0.741107 | 0.741179 | 0.741251 | 0.741323 | 0.741395 | 0.741468 | 0.741540 |
| 0.4 | 0.670384 | 0.670448 | 0.670511 | 0.670575 | 0.670639 | 0.670703 | 0.670767 | 0.670831 | 0.670894 | 0.670958 |
| 0.5 | 0.606587 | 0.606644 | 0.606700 | 0.606757 | 0.606813 | 0.606870 | 0.606926 | 0.606983 | 0.607040 | 0.607096 |
| 0.6 | 0.548862 | 0.548912 | 0.548962 | 0.549012 | 0.549062 | 0.549113 | 0.549163 | 0.549213 | 0.549263 | 0.549314 |
| 0.7 | 0.496630 | 0.496674 | 0.496719 | 0.496764 | 0.496808 | 0.496853 | 0.496897 | 0.496942 | 0.496987 | 0.497031 |
| 0.8 | 0.449369 | 0.449408 | 0.449448 | 0.449488 | 0.449527 | 0.449567 | 0.449607 | 0.449647 | 0.449686 | 0.449726 |
| 0.9 | 0.406605 | 0.406640 | 0.406676 | 0.406711 | 0.406747 | 0.406782 | 0.406817 | 0.406853 | 0.406888 | 0.406923 |
| 1 | 0.367911 | 0.367943 | 0.367974 | 0.368006 | 0.368037 | 0.368069 | 0.368100 | 0.368132 | 0.368164 | 0.368195 |
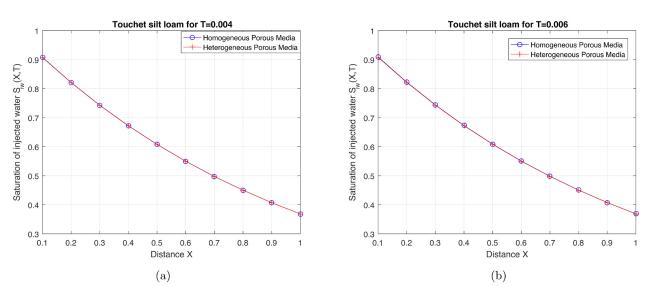
Fig.7 Water saturation vs. distance in Touchet silt loam for fixed time (a) (b) . |
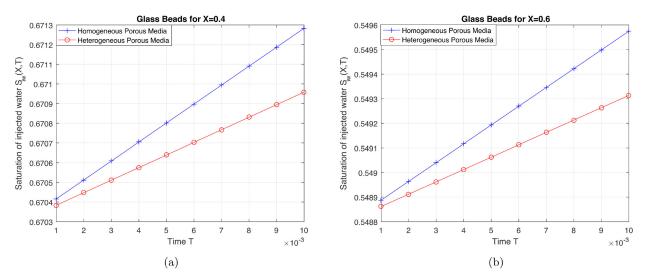
Fig.8 Water saturation vs. time in Glass beads for fixed distance (a) (b) . |
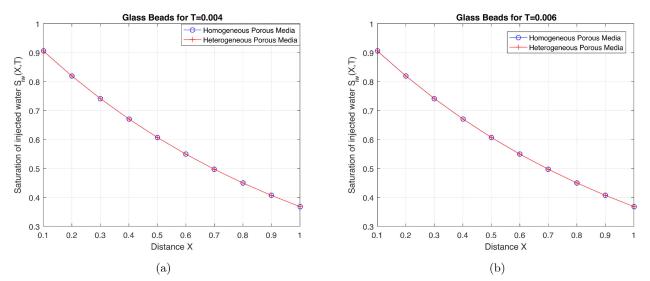
Fig.9 Water saturation vs. distance in Glass beads for fixed time (a) (b) . |
5.2. Effect of capillary pressure and heterogeneity on saturation rate
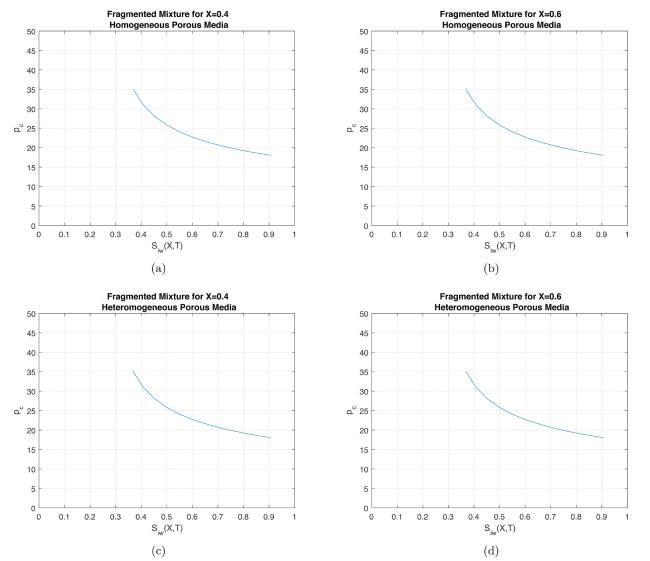
Fig.10 Comparison between capillary pressure vs. water saturation in Fragmented mixture for fixed (a) (b) , for homogeneous porous media and for fixed (c) , (d) , for heterogeneous porous media. |
Table 9 Capillary pressure vs. water saturation in Fragmented mixture, Touchet silt loam, and Glass beads. |
| Fragmented mixture | Touchet silt loam | Glass beads | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Homogeneous porous media | Heterogeneous porous media | Homogeneous porous media | Heterogeneous porous media | Homogeneous porous media | Heterogeneous porous media | ||||||
| 0.906501 | 18.04297 | 0.905958 | 18.04834 | 0.907922 | 80.76708 | 0.906998 | 80.83147 | 0.905389 | 29.43685 | 0.905208 | 29.43774 |
| 0.820160 | 18.98625 | 0.819686 | 18.99197 | 0.821317 | 87.50868 | 0.820530 | 87.57734 | 0.819219 | 29.88775 | 0.819057 | 29.88865 |
| 0.742049 | 20.03201 | 0.741634 | 20.03819 | 0.742990 | 95.19552 | 0.742320 | 95.26975 | 0.741252 | 30.35093 | 0.741107 | 30.35185 |
| 0.671383 | 21.20485 | 0.671019 | 21.21161 | 0.672148 | 104.0721 | 0.671575 | 104.1537 | 0.670705 | 30.82748 | 0.670575 | 30.82842 |
| 0.607451 | 22.53928 | 0.607130 | 22.54682 | 0.608073 | 114.4853 | 0.607581 | 114.5768 | 0.606873 | 31.31864 | 0.606757 | 31.3196 |
| 0.549610 | 24.08569 | 0.549328 | 24.09429 | 0.550115 | 126.9478 | 0.549693 | 127.0531 | 0.549117 | 31.8259 | 0.549012 | 31.82688 |
| 0.497280 | 25.92142 | 0.497031 | 25.93153 | 0.497690 | 142.2565 | 0.497326 | 142.3815 | 0.496857 | 32.35099 | 0.496764 | 32.352 |
| 0.449935 | 28.17327 | 0.449714 | 28.18564 | 0.450267 | 161.7341 | 0.449953 | 161.8891 | 0.449572 | 32.89599 | 0.449488 | 32.89703 |
| 0.407099 | 31.06877 | 0.406904 | 31.0848 | 0.407368 | 187.7818 | 0.407096 | 187.9864 | 0.406787 | 33.46337 | 0.406711 | 33.46444 |
| 0.368343 | 35.07412 | 0.368170 | 35.09692 | 0.368560 | 225.3588 | 0.368324 | 225.6559 | 0.368074 | 34.05614 | 0.368006 | 34.05727 |
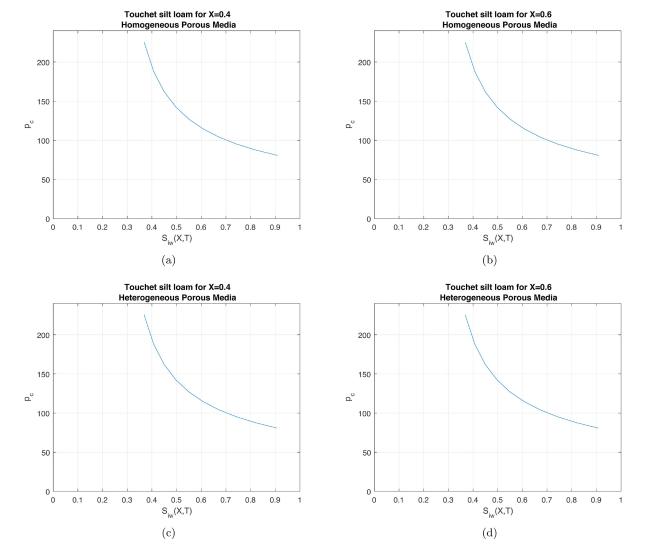
Fig.11 Comparison between capillary pressure vs. water saturation in Touchet silt loam for fixed (a) (b) , for homogeneous porous media and for fixed (c) , (d) , for heterogeneous porous media. |
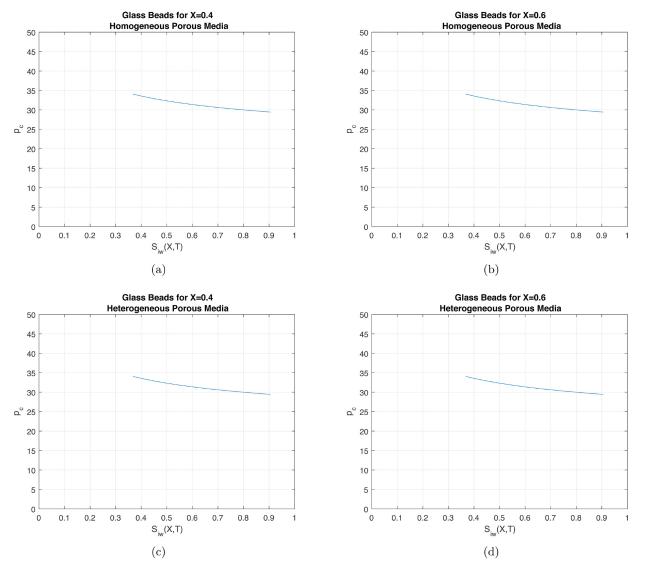
Fig.12 Comparison between capillary pressure vs. water saturation in Glass beads for fixed (a) (b) , for homogeneous porous media and for fixed (c) , (d) , for heterogeneous porous media. |
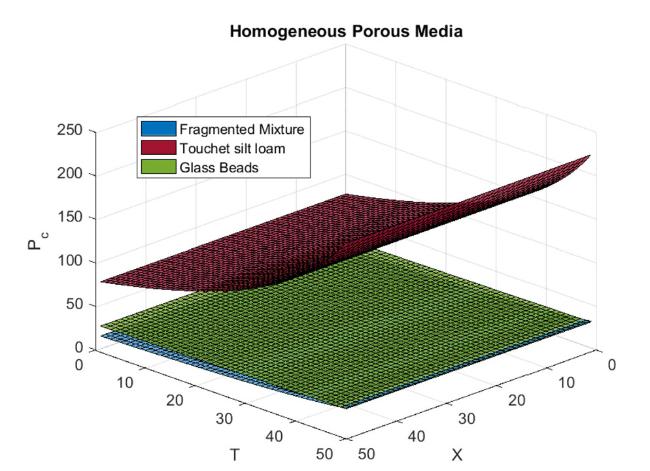
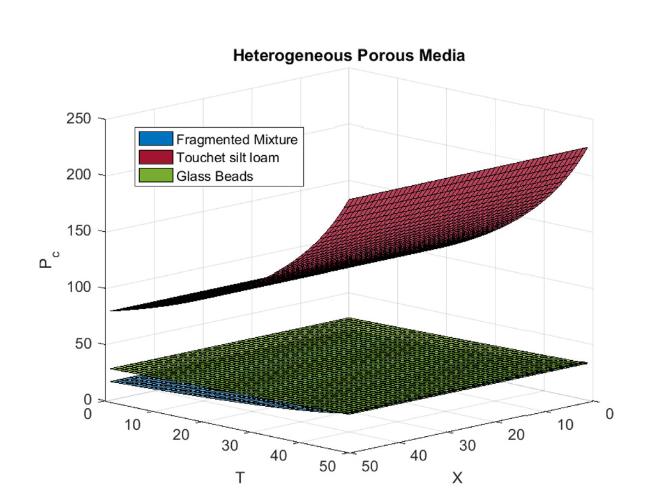
Fig.13 Comparison of capillary pressure in Fragmented mixture, Touchet silt loam and Glass beads for homogeneous porous media. |
Fig.14 Comparison of capillary pressure in Fragmented mixture, Touchet silt loam and Glass beads for heterogeneous porous media. |
Table 10 Capillary pressure vs. water saturation in Fragmented mixture, Touchet silt loam, and Glass beads. |
| Fragmented mixture | Touchet silt loam | Glass beads | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Homogeneous porous media | Heterogeneous porous media | Homogeneous porous media | Heterogeneous porous media | Homogeneous porous media | Heterogeneous porous media | ||||||
| 0.907336 | 18.0347 | 0.906521 | 18.04277 | 0.909480 | 80.65894 | 0.908087 | 80.75564 | 0.905666 | 29.43549 | 0.905394 | 29.43683 |
| 0.820877 | 18.9776 | 0.820165 | 18.98619 | 0.822621 | 87.39512 | 0.821437 | 87.4982 | 0.819464 | 29.88639 | 0.819221 | 29.88774 |
| 0.742667 | 20.02283 | 0.742043 | 20.0321 | 0.744085 | 95.07466 | 0.743076 | 95.18608 | 0.741469 | 30.34956 | 0.741251 | 30.35094 |
| 0.671916 | 21.19496 | 0.671369 | 21.20511 | 0.673069 | 103.9414 | 0.672206 | 104.0638 | 0.670898 | 30.82609 | 0.670703 | 30.8275 |
| 0.607912 | 22.52843 | 0.607431 | 22.53974 | 0.608849 | 114.3411 | 0.608110 | 114.4784 | 0.607044 | 31.31724 | 0.606870 | 31.31867 |
| 0.550010 | 24.07351 | 0.549587 | 24.08641 | 0.550771 | 126.7848 | 0.550136 | 126.9426 | 0.549269 | 31.82447 | 0.549113 | 31.82594 |
| 0.497628 | 25.90732 | 0.497254 | 25.92248 | 0.498245 | 142.0663 | 0.497698 | 142.2536 | 0.496994 | 32.34953 | 0.496853 | 32.35104 |
| 0.450238 | 28.15628 | 0.449907 | 28.17481 | 0.450738 | 161.5023 | 0.450266 | 161.7346 | 0.449693 | 32.89448 | 0.449567 | 32.89605 |
| 0.407364 | 31.04705 | 0.407071 | 31.07107 | 0.407769 | 187.4814 | 0.407360 | 187.7876 | 0.406896 | 33.46182 | 0.406782 | 33.46344 |
| 0.368575 | 35.04364 | 0.368315 | 35.07778 | 0.368902 | 224.9304 | 0.368548 | 225.3747 | 0.368171 | 34.05454 | 0.368069 | 34.05622 |
5.3. Effect of relative permeability and heterogeneity on Saturation rate
Fig.15 Comparison between relative permeability vs. water saturation in Fragmented mixture for homogeneous porous media for fixed (a) (b) , for homogeneous porous media and for fixed (c) , (d) , for heterogeneous porous media. |
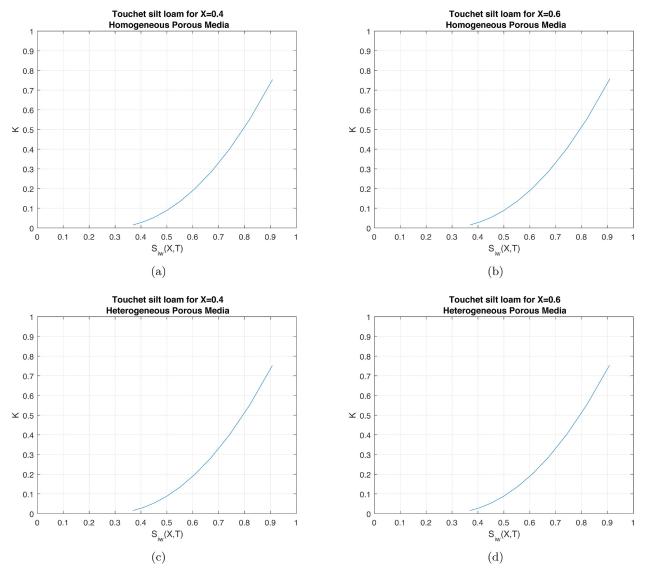
Fig.16 Comparison between relative permeability vs. water saturation in Touchet silt loam for fixed (a) (b) , for homogeneous porous media and for fixed (c) , (d) , for heterogeneous porous media. |
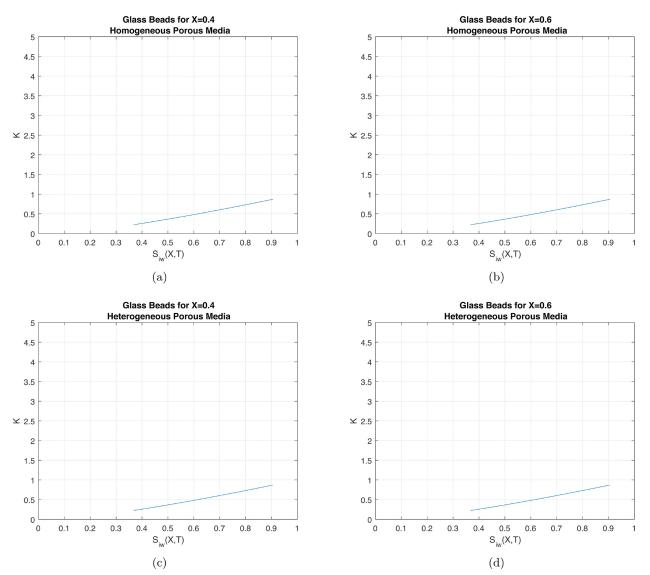
Fig.17 Comparison between relative permeability vs. water saturation in Glass beads for fixed (a) (b) , for homogeneous porous media and for fixed (c) , (d) , for heterogeneous porous media. |
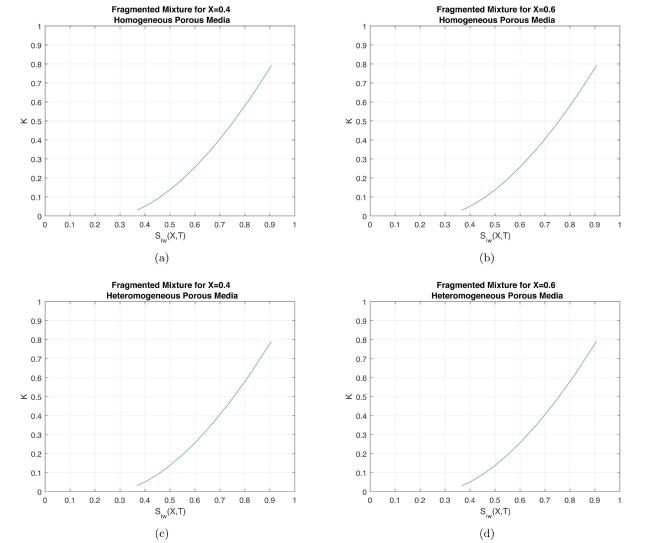
Fig.18 Comparison of relative permeability in Fragmented mixture, Touchet silt loam and Glass beads for homogeneous porous media. |
Fig.19 Comparison of relative permeability in Fragmented mixture, Touchet silt loam and Glass beads for heterogeneous porous media. |
Table 11 Relative permeability vs. water saturation in Fragmented Mixture, Touchet silt loam, and Glass beads. |
| Fragmented mixture | Touchet silt loam | Glass beads | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Homogeneous porous media | Heterogeneous porous media | Homogeneous porous media | Heterogeneous porous media | Homogeneous porous media | Heterogeneous porous media | ||||||
| 0.906501 | 0.791386 | 0.905958 | 0.790234 | 0.907922 | 0.753527 | 0.906998 | 0.751236 | 0.905389 | 0.870187 | 0.905208 | 0.869942 |
| 0.820160 | 0.616832 | 0.819686 | 0.615923 | 0.821317 | 0.554752 | 0.820530 | 0.553092 | 0.819219 | 0.755465 | 0.819057 | 0.755253 |
| 0.742049 | 0.474571 | 0.741634 | 0.473856 | 0.742990 | 0.402179 | 0.742320 | 0.400983 | 0.741252 | 0.654789 | 0.741107 | 0.654604 |
| 0.671383 | 0.359307 | 0.671019 | 0.358747 | 0.672148 | 0.2861 | 0.671575 | 0.285245 | 0.670705 | 0.566471 | 0.670575 | 0.566311 |
| 0.607451 | 0.266598 | 0.607130 | 0.266162 | 0.608073 | 0.198751 | 0.607581 | 0.198146 | 0.606873 | 0.489028 | 0.606757 | 0.488889 |
| 0.549610 | 0.192722 | 0.549328 | 0.192386 | 0.550115 | 0.133932 | 0.549693 | 0.133509 | 0.549117 | 0.421154 | 0.549012 | 0.421033 |
| 0.497280 | 0.134568 | 0.497031 | 0.134312 | 0.497690 | 0.086696 | 0.497326 | 0.086406 | 0.496857 | 0.361698 | 0.496764 | 0.361593 |
| 0.449935 | 0.089543 | 0.449714 | 0.089351 | 0.450267 | 0.053102 | 0.449953 | 0.052908 | 0.449572 | 0.309651 | 0.449488 | 0.30956 |
| 0.407099 | 0.055497 | 0.406904 | 0.055357 | 0.407368 | 0.030018 | 0.407096 | 0.029893 | 0.406787 | 0.264122 | 0.406711 | 0.264042 |
| 0.368343 | 0.030672 | 0.368170 | 0.030575 | 0.368560 | 0.014954 | 0.368324 | 0.014879 | 0.368074 | 0.224328 | 0.368006 | 0.224259 |
Table 12 Relative permeability vs. water saturation in Fragmented mixture, Touchet silt loam, and Glass beads. |
| Fragmented mixture | Touchet silt loam | Glass beads | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Homogeneous porous media | Heterogeneous porous media | Homogeneous porous media | Heterogeneous porous media | Homogeneous porous media | Heterogeneous porous media | ||||||
| 0.907336 | 0.79316 | 0.906521 | 0.791428 | 0.909480 | 0.757393 | 0.908087 | 0.753935 | 0.905666 | 0.87056 | 0.905394 | 0.870192 |
| 0.820877 | 0.618208 | 0.820165 | 0.616841 | 0.822621 | 0.55751 | 0.821437 | 0.555006 | 0.819464 | 0.755786 | 0.819221 | 0.755467 |
| 0.742667 | 0.475636 | 0.742043 | 0.474561 | 0.744085 | 0.404135 | 0.743076 | 0.402331 | 0.741469 | 0.655064 | 0.741251 | 0.654788 |
| 0.671916 | 0.360127 | 0.671369 | 0.359286 | 0.673069 | 0.287477 | 0.672206 | 0.286187 | 0.670898 | 0.566709 | 0.670703 | 0.566469 |
| 0.607912 | 0.267227 | 0.607431 | 0.266571 | 0.608849 | 0.19971 | 0.608110 | 0.198797 | 0.607044 | 0.489233 | 0.606870 | 0.489024 |
| 0.550010 | 0.1932 | 0.549587 | 0.192694 | 0.550771 | 0.134591 | 0.550136 | 0.133953 | 0.549269 | 0.42133 | 0.549113 | 0.421149 |
| 0.497628 | 0.134927 | 0.497254 | 0.134541 | 0.498245 | 0.08714 | 0.497698 | 0.086703 | 0.496994 | 0.361851 | 0.496853 | 0.361693 |
| 0.450238 | 0.089807 | 0.449907 | 0.089519 | 0.450738 | 0.053394 | 0.450266 | 0.053102 | 0.449693 | 0.309782 | 0.449567 | 0.309646 |
| 0.407364 | 0.055687 | 0.407071 | 0.055477 | 0.407769 | 0.030202 | 0.407360 | 0.030014 | 0.406896 | 0.264235 | 0.406782 | 0.264116 |
| 0.368575 | 0.030803 | 0.368315 | 0.030657 | 0.368902 | 0.015063 | 0.368548 | 0.01495 | 0.368171 | 0.224426 | 0.368069 | 0.224323 |