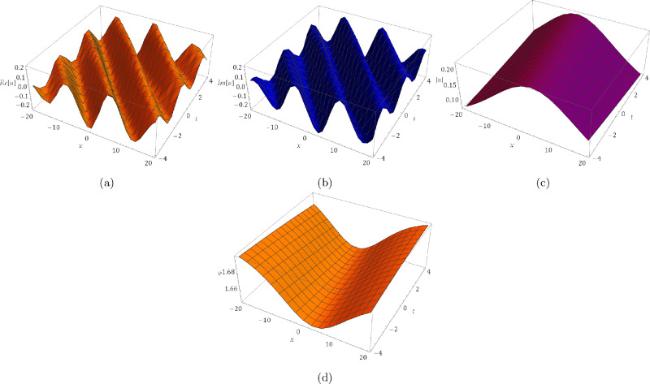
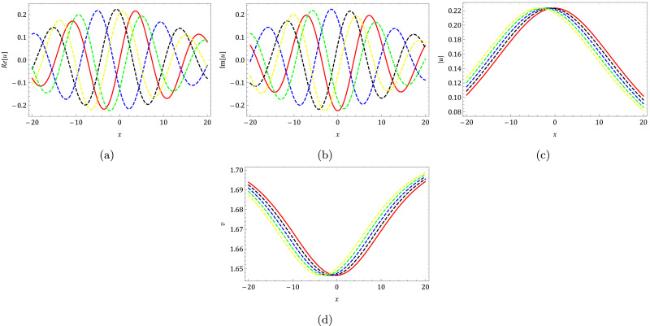
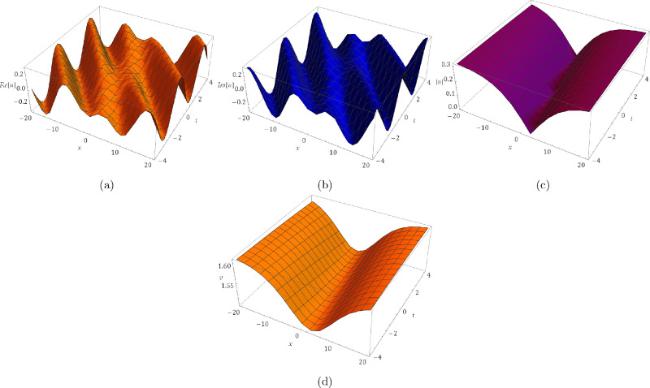
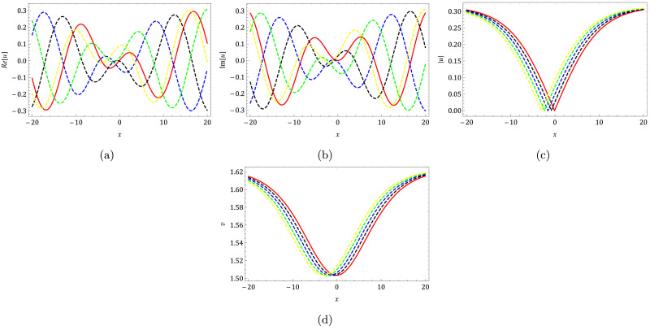
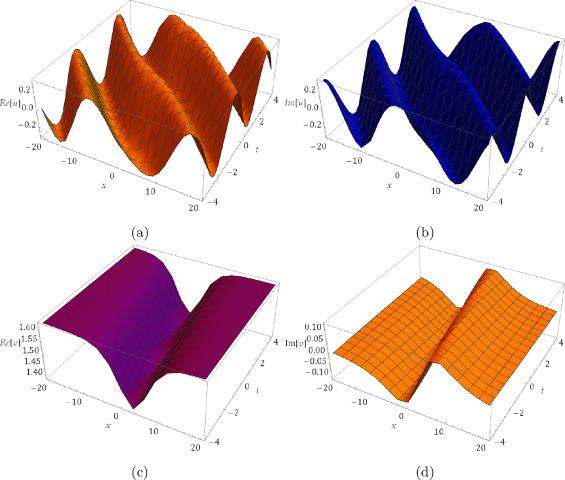
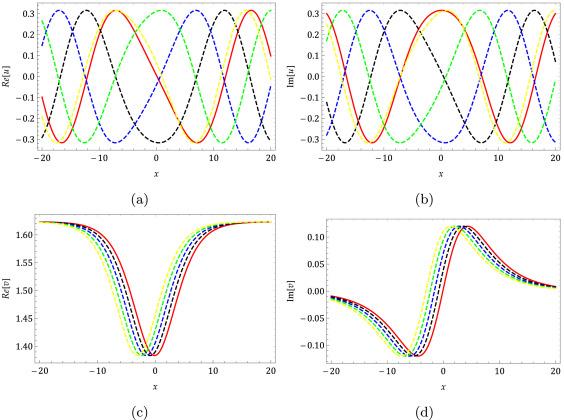
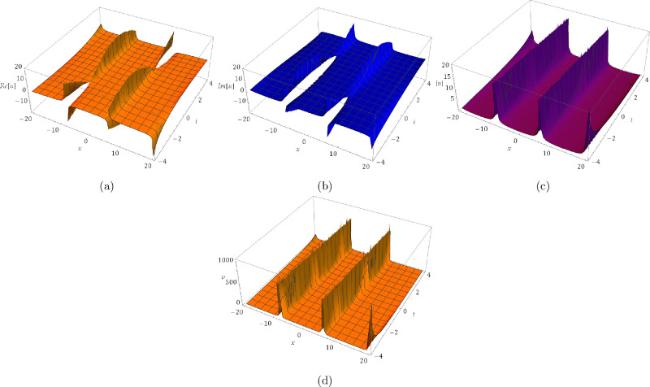
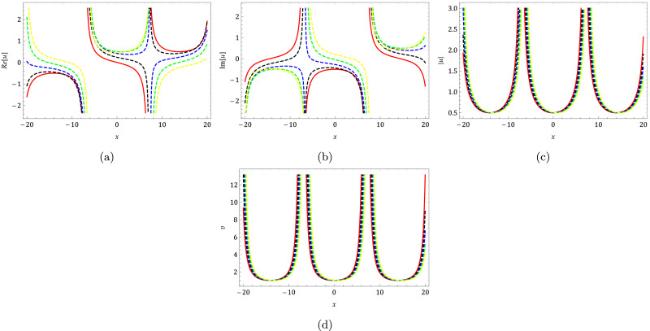
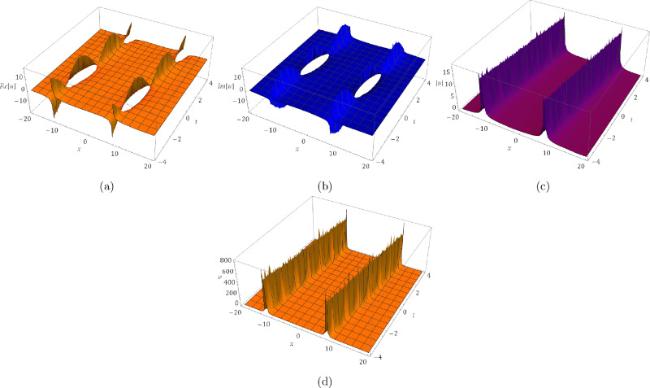
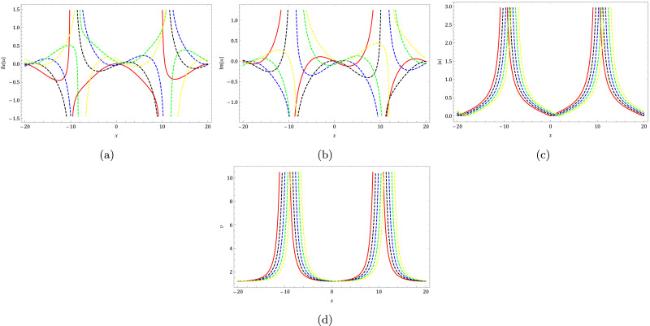
where
represents a complex function, and
represents a real-valued function. The variables
and
are all real constants. In addition,
denotes the short wave, and
represents the long wave. In
[39],
[40], the existence of solutions for the Eq. (1) was highlighted. The applications of Kudryashov and sub-equation methods to the proposed system have been published in Akinyemi et al.
[41]. The numerical soutions with the help of q-homotopy analysis transform method was reported in Akinyemi et al.
[42]. However, our aim is to further complement our previous study on Eq. (1) by proposing a modified Sardar sub-equation (MSSE) procedure to study this coupled system. The proposed method is an innovative technique for obtaining exact solutions to differential equations. It provides a straightforward approach for dealing with nonlinear evolution equation solutions. The SSE method has been used to obtain desirable findings and assistance in the investigation of solutions to numerous problems that have arisen in applied mathematics and physics
[43],
[44],
[45]. Other advantage of this method is that it contain solutions reported in Akinyemi et al.
[41],
42] and many other new soliton type solutions. These types of solutions are essential because they can aid in the understanding of several physical processes connected to wave propagation. It is important to highlight that the results acquired in this study are completely new and has never been published before. Kumar et al.
[14] used the sine-Gordon equation approach to investigate the generalized Schrödinger–Boussinesq equations, which is another coupled model that describes the interaction between complex short and real long waves envelope.