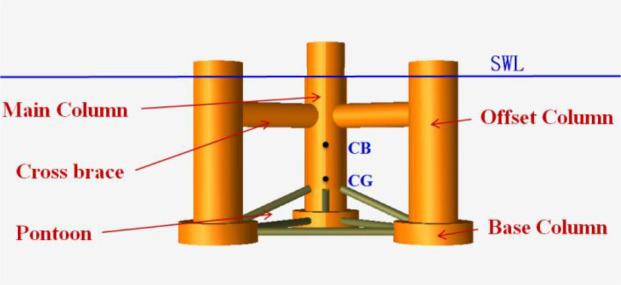
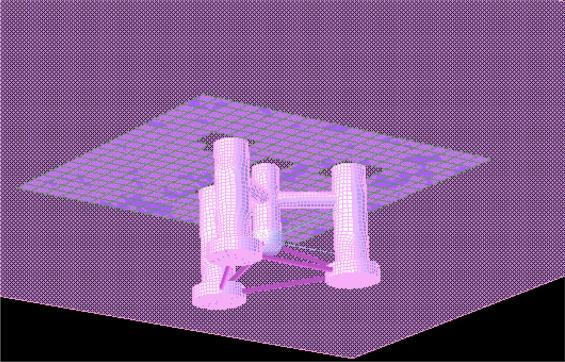
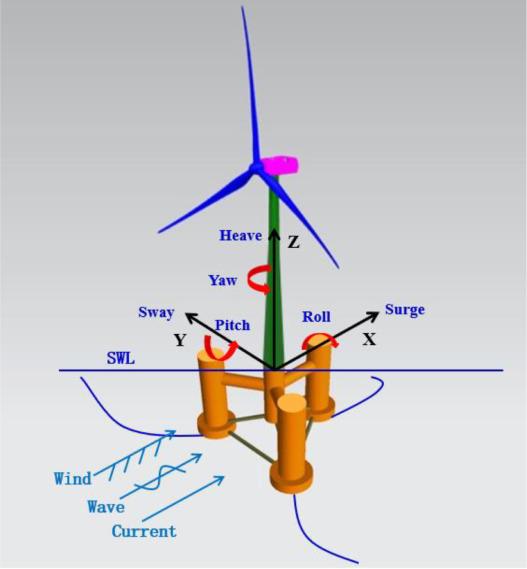
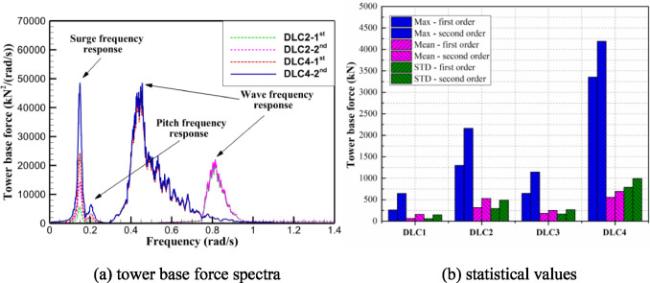
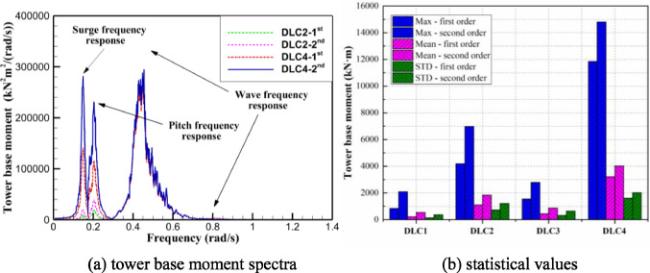
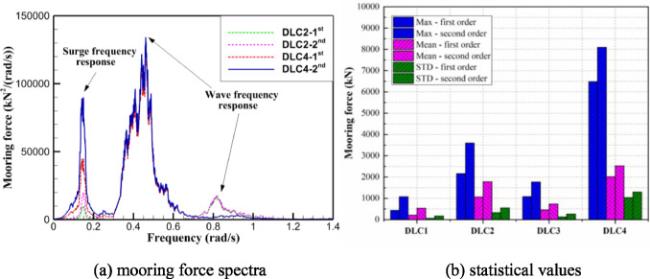
Due to the shortage of several classical floating foundations, the intent of this research study is to provide and validate a multi-column platform concept with low CG that combines the advantages of semi-submersible floating foundation and spar type floating foundation, as shown in
Fig. 1. The multi-column low CG platform is designed to support a 6MW wind turbine class
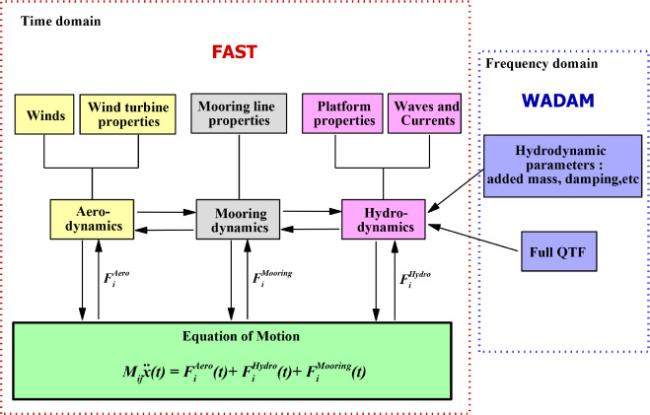
[18] and operate at a water depth of 50m in the South China Sea. The concept of the multi-column low CG platform (multi-column deep-draft platform) has a deeper draft than a typical semi-submersible floating foundation. The CB of the platform is increased by using large diameter cylindrical cross braces below the still water line (SWL), which providing a certain buoyancy, thus reducing the diameter of the offset columns (can be regarded as a short SPAR). In addition, the CG of the platform is lowered by using large diameter base columns as ballast tanks, and the bottom ballast also effectively increases the heave damping. With the above changes, the CG of the multi-column deep-draft platform concept is much lower than the CB, which satisfies the stability requirement of the platform and solves the disadvantage that the SPAR platform cannot be applied in shallow water. To verify the viability of the multi-column deep-draft platform, the coupled dynamic responses of the FOWT system are simulated by the time domain software FAST
[19] and the frequency domain software WADAM
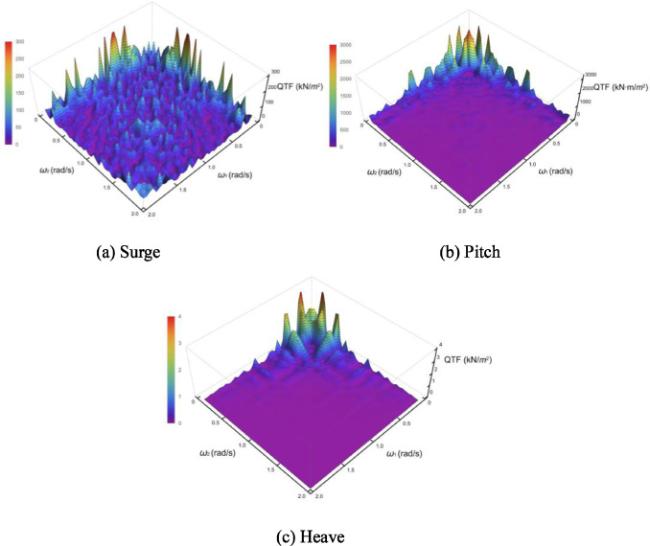
[20]. In addition, the effect of the second-order wave force may increase with the decreasing of water depth, because a lower water depth is usually associated to a lower natural period [
21,
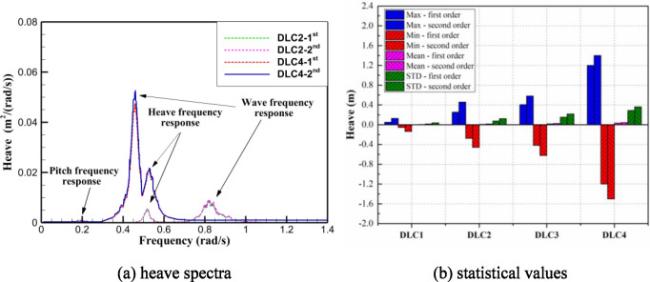
22]. Thus, the effect of second-order wave load is considered in the simulation model and the results are compared and analyzed. Statistical values and spectral analysis are performed for motion response of the multi-column platform, fore-aft force and moment of the tower base and mooring force are researched respectively. The results demonstrate that the coupled dynamic responses at rated operating condition and extreme condition meet the normal operating requirements and extreme survival requirements of FOWT system in the shallow water of South China Sea. In addition, it is found that, the wave frequency response gradually replaces the second-order low frequency response as the main influencing factor of the coupled dynamic response of the FOWT system with the increasing severity of the sea states. However, in general, the magnitude of second-order low frequency response increase with the increasing severity of the design load cases. Thus, in the subsequent design of the shallow water FOWT system, the second-order effects should be paid enough attention.