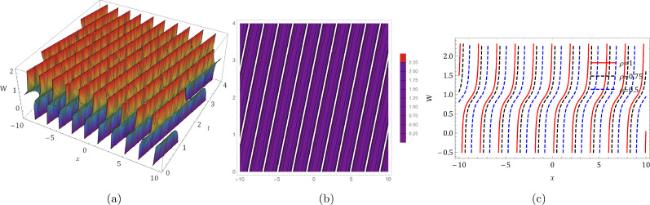
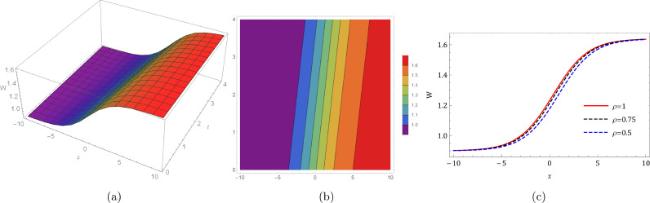
where
and
are nonzero real parameters and
(
) is the fractional order. Therefore, in the study the conformable derivative (CD) will be explored. The fundamental reason for examining this sort of local derivative is that, when compared to other fractional derivative definitions, the CD can meet numerous properties spanning the chain, product, or quotient rules. To exact the dark solitons, singular solitons, periodic wave, and rational form solutions under certain parametric conditions, we employed two novel integrable techniques. These methods are the sub-equation and generalized Kudryashov methods which have been applied many times for solving strong nonlinear models in the field of applied sciences and engineering. The sub-equations method has been used to find soliton solution type different type of equations including space time-fractional equation
[40], perturbed nonlinear Schrödinger
[23], conformable fractional PDE
[41], and others. Also, the generalized Kudryashov method have been used to solve other type of equations including fractional mathematical biology problems
[42], coupled sine Gordon equations
[43], fractional Boussinsque equations
[44], fractional Klein Gordo equation
[45], Cahn Hilliard equations
[46], Kuramoto-Sivashinsky equation
[47], many other equations that can be found in
[48],
[49], and references therein. It should be emphasized that the discovery of new models that incorporates soliton-type solutions are an intriguing outcome that will also aid future research in numerous fields of applied science and engineering.