For addressing Cauchy problems for ordinary and partial differential equations, classical methods like as the Laplace method and the Fourier transform approach were developed. In recent soliton theory [1], [2], Cauchy issues for nonlinear ordinary and partial differential equations have been solved using isomonodromic transformation and inverse scattering methods. One of the most fascinating and promising scientific research areas is the study of exact solutions and the associated challenge of providing results for a wide class of nonlinear equations [3].

Exact solutions to partial differential equations have significant mathematical and physical aspects. In both time and space, a soliton solution is a wave solution with exponentially localized functions in all directions. Exact solutions to partial differential equations have significant mathematical and physical aspects. In addition, interaction solutions between lump and soliton solutions are well-known for allowing nonlinear processes to be shown.

Internal waves and ocean topography have been a major focus of research for a long time. The driving mechanism of wave solutions affects the propagation of surface and internal gravity waves. Oceans, lakes, and the sky all have these waves, and the mechanism that creates them could be beneficial in ocean engineering. Shallow-water equations are a collection of hyperbolic partial differential equations that explain fluid flow beneath a pressure surface [4]. Water wave dispersion refers to frequency dispersion in fluid dynamics, which means waves of different wavelengths travel at varying phase speeds. In this context, water waves are waves that propagate on the water's surface, with gravity and surface tension acting as restoring forces. As a result, water with a free surface is commonly thought of as a dispersive medium [5]. Ocean engineering involves the development, design, operation, and maintenance of watercraft propulsion and ocean systems using a variety of engineering sciences such as mechanical engineering, electrical engineering, electronic engineering, and computer science. 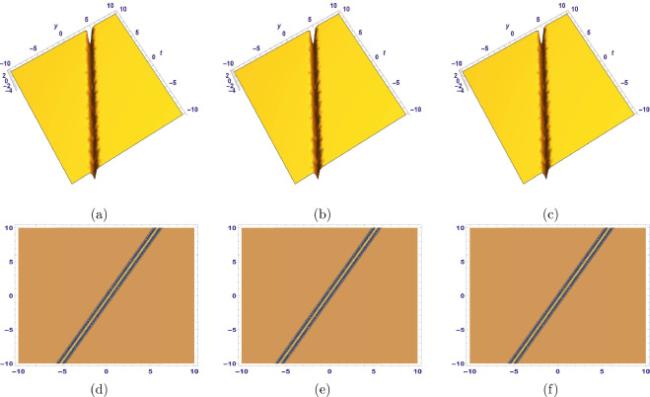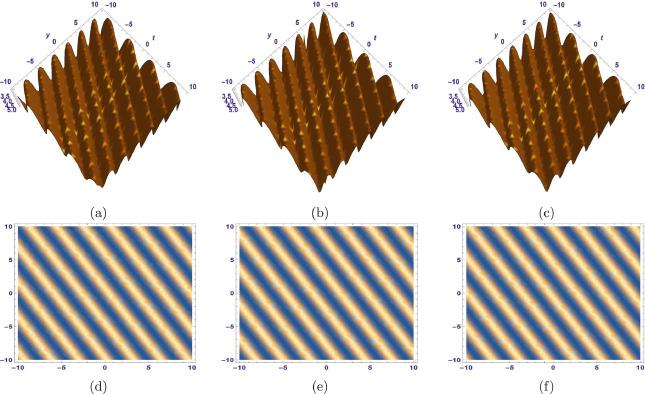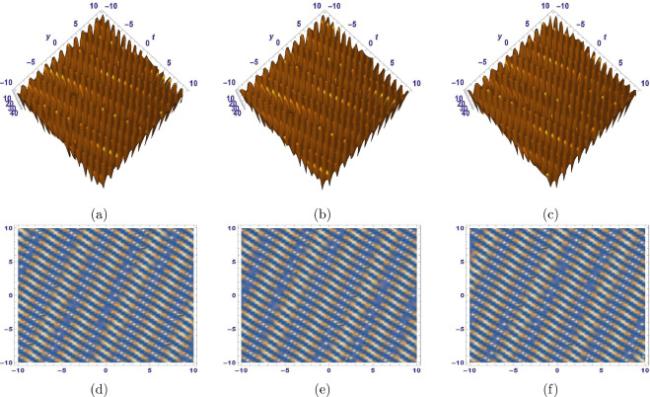Power and propulsion plants, machinery, piping, automation and control systems for all types of marine vehicles, as well as coastal and offshore constructions, are all included [6]. Water wave equations describe various nonlinear physical phenomena in the above mentioned areas. Breather wave solutions, for example, are crucial in the study of ocean waves since they are formed from these types of equations. Breathers are pulsating localized structures that have been used to simulate high waves in a variety of nonlinear dispersive environments. They are commonly used in coastal engineering. They use a narrow banded beginning procedure to replicate severe waves in a range of nonlinear dispersive mediums. Breathers, on the other hand, may be able to exist in more complex ecosystems, such as random seas, despite the inherent physical limitations, according to several recent studies [7]. This study is going to present some important two-wave and breather wave solutions to the (2+1)-dimensional Korteweg-de Vries equation.

The study of many complicated physical aspects and other nonlinear engineering difficulties, such as lump solutions, kink solutions, and so on, relies heavily on these solutions and their generalized forms. Lump type solutions have been developed and their dynamics examined for a number of nonlinear equations. The study of lump-kink solutions, or the collisions between lump and kink solutions, has piqued the curiosity of many researchers [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21]. Lump solutions, on the other hand, are very different and haven't been thoroughly investigated. There exist prerequisites for a high number of nonlinear equation solutions in this regard. This prompted us to look for lump interaction complexitons solutions to the (2+1)-dimensional Korteweg-de Vries equation in plasmas with an electrostatic wave potential. The (2+1)-dimensional KdV equation describes the electrostatic wave potential in plasmas [22]

Consider the variable transformation

Plugging (2) into (1), the following bilinear form is secured

Equation (3) may equivalently be written in Hirota's operators form as [22]

In this section, we successfully construct two-wave solutions. We use the following test function to ensure that the two-wave solutions are secured:

Plugging (5) into (3), provides a polynomial in exponential, trigonometric and hyperbolic functions. The following collection of solutions are obtained by solving a system of algebraic equations collected based on the powers of the exponential, trigonometric and hyperbolic functions:

(I): ${\gamma }_2=\frac{3k-4{\gamma }_1}{{\gamma }_1},{\gamma }_3=\frac{2\sqrt{{\gamma }_1^{3}k-{\gamma }_1^4}+{\gamma }_{1}k}{k-2{\gamma }_1},{\gamma }_4=\frac{3{\gamma }_{1}k-6\sqrt{{\gamma }_1^3(k-{\gamma }_1)}}{{\gamma }_1^2}-2,{\gamma }_5={\gamma }_1,{\gamma }_6=\frac{3k-4{\gamma }_1}{{\gamma }_1},{\delta }_3=0.$

(II): ${\gamma }_1=-{\gamma }_3,{\gamma }_2=\frac{2{\gamma }_3+3k}{{\gamma }_3},{\gamma }_4=\frac{-2{\gamma }_3-3k}{{\gamma }_3},{\delta }_1=\frac{{\delta }_3^2}{4{\delta }_2},{\delta }_4=0.$ .

Considering set-I, we provide

Thus,

where ${\varphi }_1=\frac{t(3k-4{\gamma }_1)}{{\gamma }_1}+x+{\gamma }_{1}y$ .

Considering set-II, we provide

Thus,

where ${\varphi }_2=\frac{t(2{\gamma }_3+3k)}{{\gamma }_3}+x-{\gamma }_{3}y,{\varphi }_3=\frac{t(-2{\gamma }_3-3k)}{{\gamma }_3}+x+{\gamma }_{3}y$ .

We use the following test function to ensure that the breather wave solutions are secured:

Plugging (10) into (3), the following collection of solutions are obtained by conducting some symbolic computations:

(I): ${\beta }_0=3k+3p_0^2-p_1^2,{\lambda }_0=3k+p_0^2-3p_1^2,{\eta }_2=-\frac{{\eta }_1^2{p}_0^2}{4p_1^2}.$

(II): $p_1=i{p}_0,{\beta }_0=6k-{\lambda }_0+8p_0^2,{\eta }_2=\frac{{\eta }_1^2}{4}.$

(III) $p_1=-i{p}_0,{\beta }_0=3k+4p_0^2,{\lambda }_0=3k+4p_0^2.$

Considering set-I, we provide

Thus,

where ${\varphi }_4=p_1(t(3k+3p_0^2-p_1^2)+x+y),{\varphi }_5=p_0(t(3k+p_0^2-3p_1^2)+x+y).$

Considering set-II, we provide

Thus,

where ${\varphi }_6=i{p}_0(t(6k-{\lambda }_0+8p_0^2)+x+y).$

Considering set-III, we provide

Thus,

where ${\varphi }_7=i{p}_0(t(3k+4p_0^2)+x+y),{\varphi }_8=p_0(t(3k+4p_0^2)+x+y).$

Generally, the Korteweg De Vries equation is a mathematical model of waves on shallow water surfaces used in mathematics. It is renowned as the classic example of a perfectly solvable model whose solutions can be described precisely and precisely. Via the properties of Bell's polynomial, Wang et al. [22] gave the general lump solutions, lumpoff solutions, and rogue wave solutions to (1). Rosa et al. [23] presented the exact solutions of (1) via Lie symmetry analysis. Wazwaz [24] provided single and multiple-soliton solutions to (1) via tanh-coth method and the cosh ansatz. The (2+1)-dimensional KdV equation with plasma electrostatic wave potential has been studied in this paper. The bilinear Hirota technique is used to effectively design new lump interaction complexions. The evaluated nonlinear model was fulfilled by all of the recorded solutions. Numerical simulations of the resulting results are also shown using 3-dimensional and contour graphs. The findings given in this study have never been published before, to the best of our knowledge (Fig. 1, Fig. 2, Fig. 3, Fig. 4).

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.