1. Introduction
2. Lie symmetry analysis of Eq. (1)
2.1. Symmetry groups
3. One-dimensional optimal system
3.1. Calculation of the invariants
Table 1 Commutator table . |
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | |||||||
| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 |
3.2. Construction of the adjoint transformation matrix
Table 2 Adjoint representation table. |
3.3. Optimal system
3.4. Similarity reductions and exact solutions
4. Soliton solutions
4.1. Similarity reduction from translational symmetries
4.2. Solutions of Eq. (78) by new auxiliary method
4.3. Graphical results
4.3.1. Graphic description
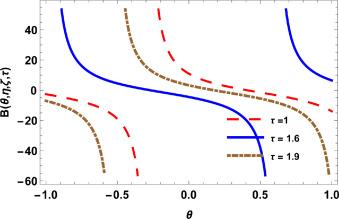
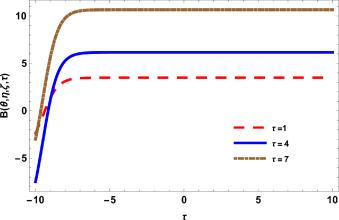
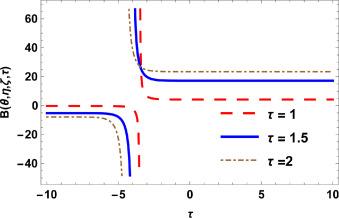
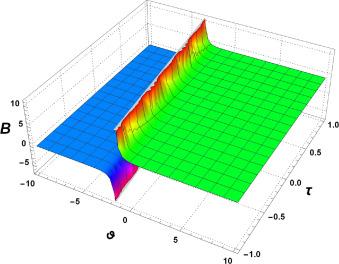
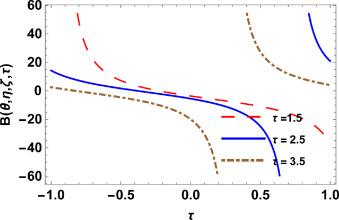
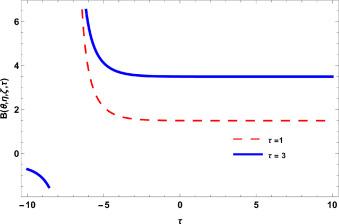
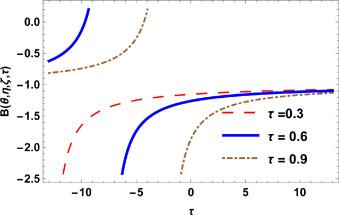
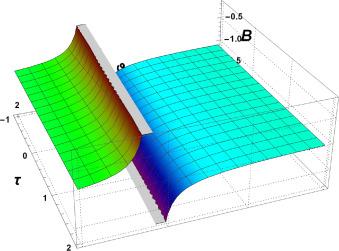
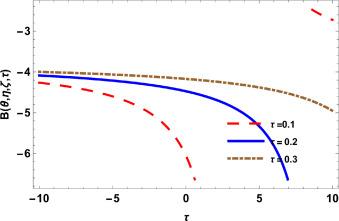
Fig.1 2D Graphics. |
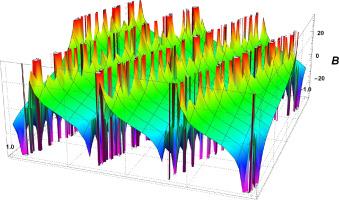
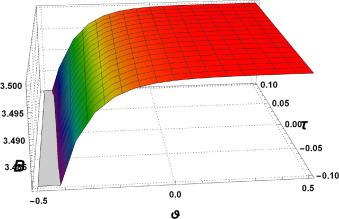
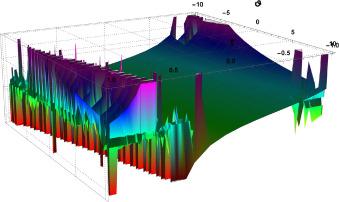
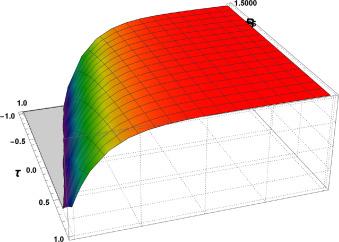
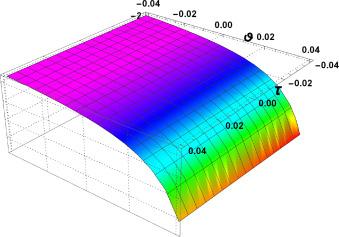
Fig.2 3D Graphics. Graphical interpretation of for , , , , , , and , . |
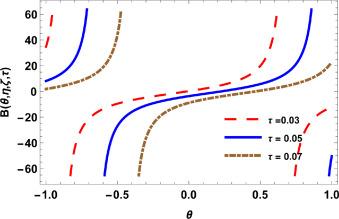
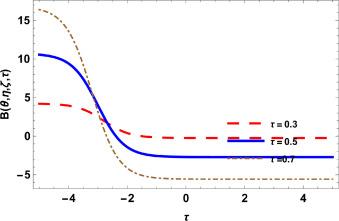
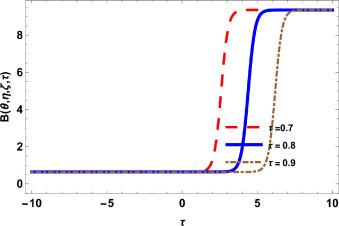
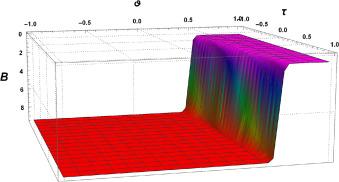
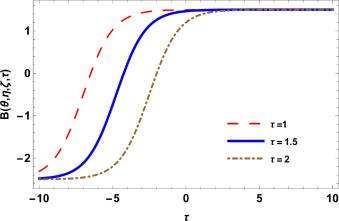
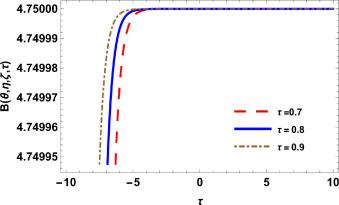
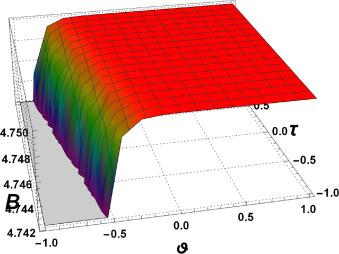
Fig.3 2D Graphics. |
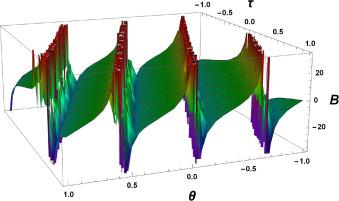
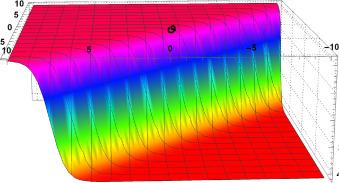
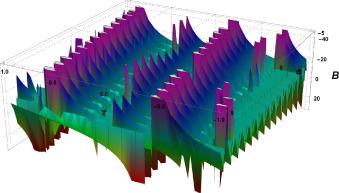
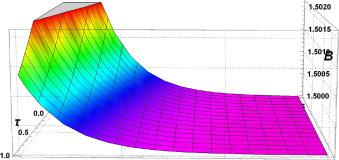
Fig.4 3D Graphics. Graphical interpretation of for , , , , , , , and . |
Fig.5 2D Graphics. |
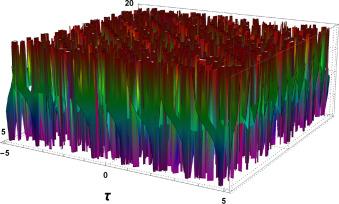
Fig.6 3D Graphics. Graphical interpretation of for , , , , , , , and . |
Fig.7 2D Graphics. |
Fig.8 3D Graphics. Graphical interpretation of for , , , , , , , , and . |
Fig.9 2D Graphics. |
Fig.10 3D Graphics. Graphical interpretation of for , , , , , , , , and . |
Fig.11 2D Graphics. |
Fig.12 3D Graphics. Graphical interpretation of for , , , , , , , , and . |
Fig.13 2D Graphics. |
Fig.14 3D Graphics. Graphical interpretation of for , , , , , , , , and . |
Fig.15 2D Graphics. |
Fig.16 3D Graphics. Graphical interpretation of for , , , , , , , and . |
Fig.17 2D Graphics. |
Fig.18 3D Graphics. Graphical interpretation of for , , , , , , , and . |
Fig.19 2D Graphics. |
Fig.20 3D Graphics. Graphical interpretation of for , , , , , , , and . |
Fig.21 2D Graphics. |
Fig.22 3D Graphics. Graphical interpretation of for , , , , , , , , and . |
Fig.23 2D Graphics. |
Fig.24 3D Graphics. Graphical interpretation of for , , , , , , , , , and . |
Fig.25 2D Graphics. |
Fig.26 3D Graphics. Graphical interpretation of for , , , , , , , , and . |
Fig.27 2D Graphics. |
Fig.28 3D Graphics. Graphical interpretation of for , , , , , , , , and . |