1 Introduction
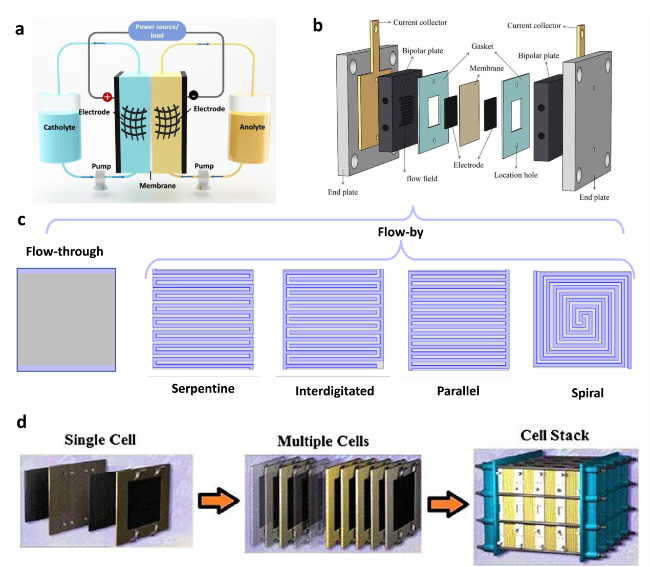
1.1 Flow fields for redox flow batteries
1.2 Critical issues in flow field design and optimization
1.2.1 Influence of flow fields on mass transport
1.2.2 Influence of flow fields on pressure drop
Table 1 Evaluation parameters of RFBs |
| Parameter | Expression |
|---|---|
| Coulombic efficiency (CE) | $CE=\frac{\int I_{d}(t)dt}{\int I_{c}(t)dt}$ |
| Energy efficiency (EE) | $EE=\frac{\int E_{d}(t)I_{d}(t)dt}{\int E_{c}(t)I_{c}(t)dt} $ |
| Voltage efficiency (VE) | $VE=\frac{\int E_{d}(t)I_{d}(t)dt/\int I_{d}(t)dt}{\int E_{c}(t)I_{c}(t)dt/\int I_{c}(t)dt}$ |
| Pumping power (Wpump) | $W_{pump}=\frac{2q\Delta P}{\varphi} $ |
| Pump-based voltage efficiency (VEpump) | $VE_{pump}=\frac{E_{d,ave}I-W_{pump}}{E_{c,ave}I+W_{pump}} $ |
| System efficiency (SE) | $SE=\frac{\int(E_{d}(t)I_{d}(t)-W_{pump})dt}{\int(E_{c}(t)I_{c}(t)+W_{pump})dt}$ |
I denotes the current, and the subscripts d and c denote the discharge and charge process. E denotes the cell potential. q denotes the flow rate, ∆P denotes the pressure drop of the system, φ denotes the pump efficiency |
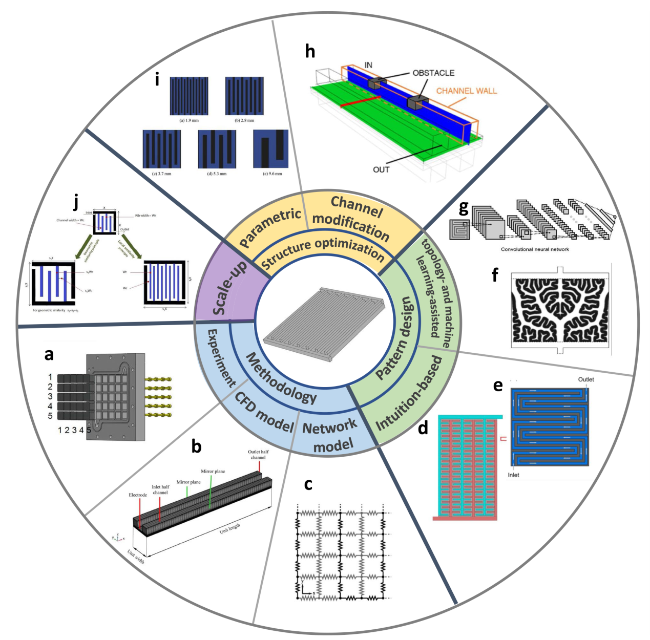
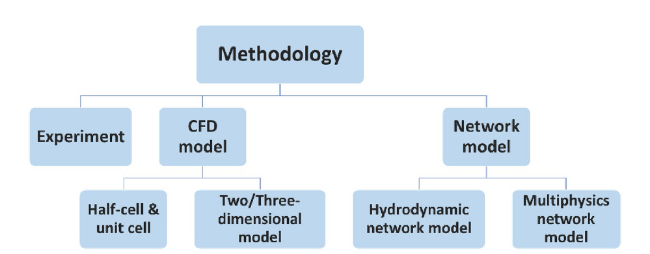
2 Methodology
Fig. 3 Outlines of methodology for evaluating flow fields |
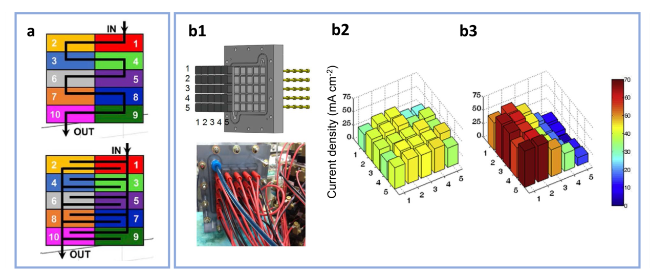
Fig. 4 a Schematic diagram of the segmented flow fields (reproduced with permission from Ref. [59]). b1 Schematics and photos of a graphite flow field plate divided into 25 segments. Current density distributions of the segmented graphite flow field plate at (b2) the beginning of the discharging process, b3 the end of the discharging process with a current density of 40 mA cm−2 (reproduced with permission from Ref. [34]) |
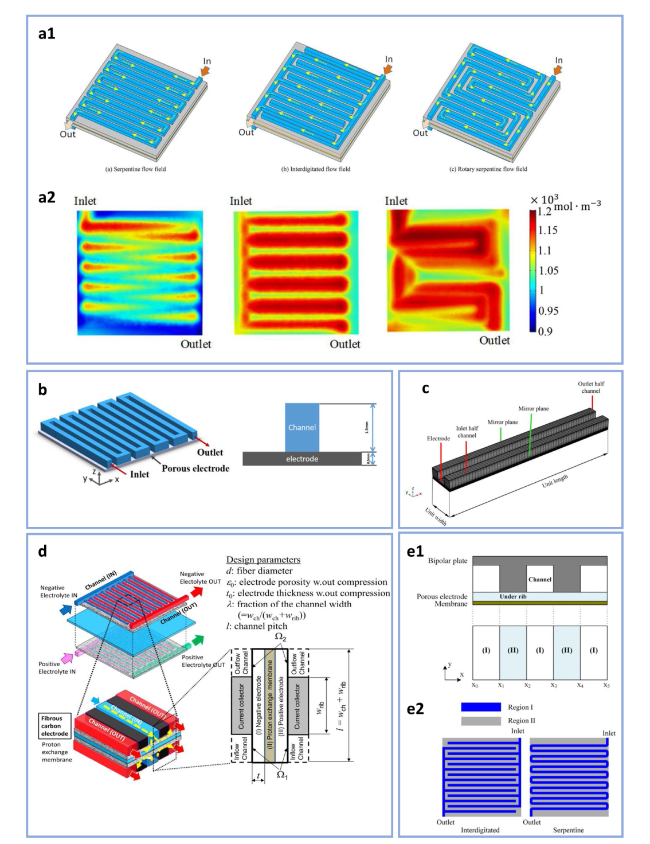
Fig. 5 a1 Three-dimensional computational domain of cells with serpentine flow field, interdigitated flow field and rotary serpentine flow field. a2 Distributions of V2+ ions concentration in the mid-thickness plane of the electrode with different flow fields at 0.8 SOC (reproduced with permission from Ref. [60]). b Schematic of half-cell three-dimensional computational domain and cross-sectional view of flow channel and electrode (reproduced with permission from Ref. [61]). c Schematic of computational domain for the unit interdigitated flow field (reproduced with permission from Ref. [62]). d Schematic view of a single RFB cell with interdigitated flow field and two-dimensional computational domain (reproduced with permission from Ref. [66]). e1 Schematics of flow field structure and computational regions. e2 Schematics of two-dimensional computational domain with two regions for interdigitated and serpentine flow fields (reproduced with permission from Ref. [23]) |
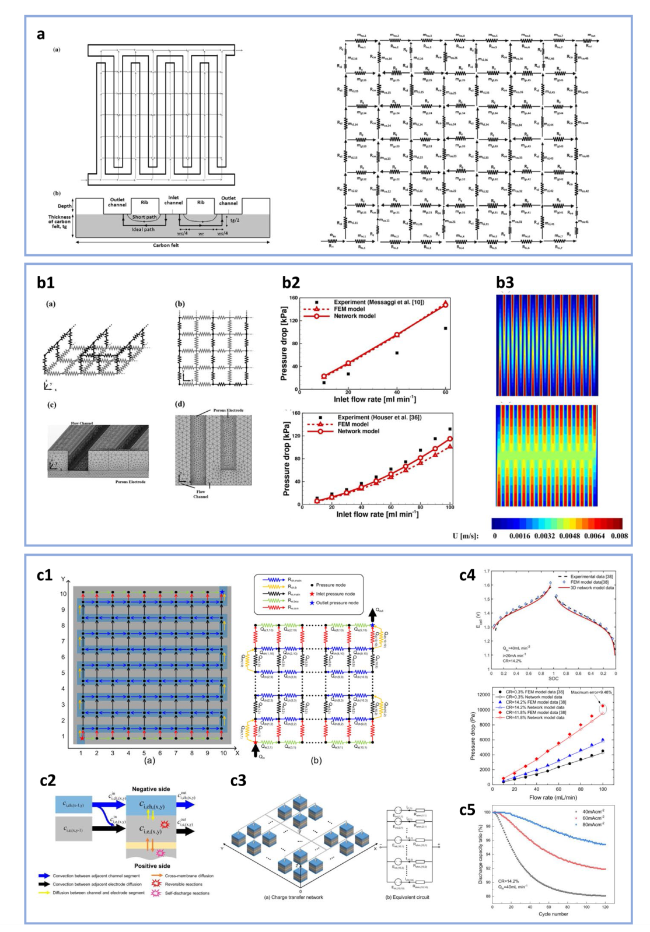
Fig. 6 a Schematic of a 4-pair segmented interdigitated flow field, transverse length through the porous electrode and hydrodynamic network diagram (reproduced with permission from Ref. [67]). b1 Computational grids for an RFB cell with serpentine flow field used in the two-layer hydrodynamic network model and FEM model. b2 Comparison of pressure drops obtained from the network model with those from experiments and FEM model with serpentine flow field. b3 X-direction velocity distribution of the FEM model (up) and two-layer network model (down) within the porous electrode with serpentine flow field at 20 mL min−1 (reproduced with permission from Ref. [35]). c1 Schematic of electrolyte flow pattern and corresponding flow resistance network. c2 Schematic of species transfer caused by the diffusion, convection between adjacent segments. c3 Schematic of charge transfer network and equivalent circuit. c4 Comparison of charge-discharge curves and pressure drops obtained from the network model with those from experiments and FEM model. c5 Predicted discharge capacity ratio at different current densities (reproduced with permission from Ref. [68]) |
3 Flow field pattern design
3.1 Classic flow field patterns
3.1.1 Flow-through and flow-by architecture
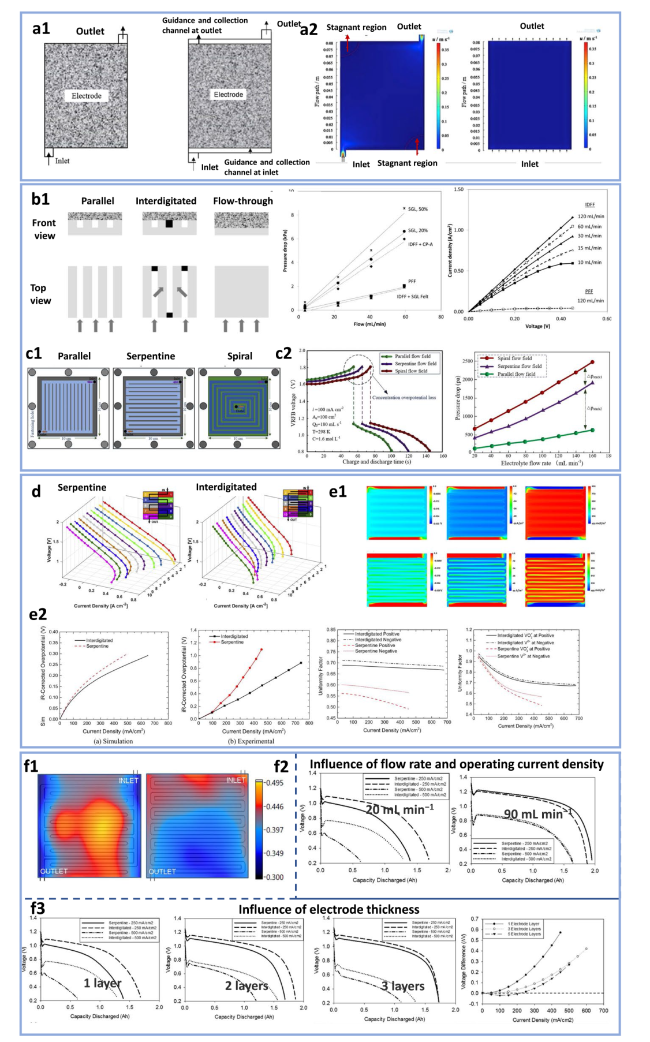
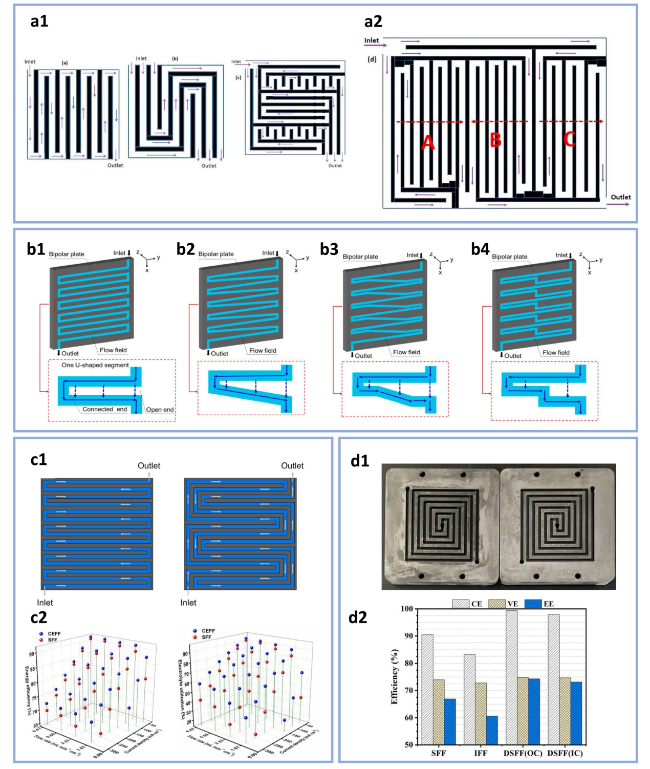
Fig. 7 Comparison between conventional cell configurations. a1, a2 Different types of inlet design for flow-through configurations (reproduced with permission from Ref. [70]), b1, b2 comparison between parallel, interdigitated and flow-through configurations (reproduced with permission from Ref. [71]), c1, c2 comparison between parallel, serpentine and spiral configurations (reproduced with permission from Ref. [29]), d local polarization curve measurement for serpentine and interdigitated flow fields (reproduced with permission from Ref. [59]), e1, e2 numerical comparison between serpentine and interdigitated flow fields (reproduced with permission from Ref. [23]), and f1-f3 influence of operating conditions and electrode properties on the comparison between serpentine and interdigitated flow field (reproduced with permission from Ref. [27]) |
3.1.2 Flow field configurations
3.2 Novel flow field patterns
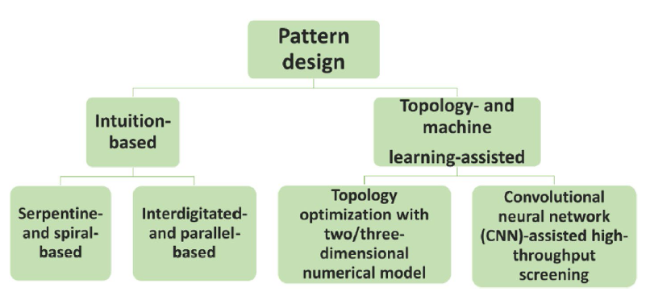
Fig. 8 Outlines for pattern design of flow fields |
3.2.1 Intuition-based flow field pattern design
Fig. 9 Schematics of (a1) single serpentine flow field, three-parallel serpentine flow field, enhanced cross-flow serpentine flow field and (a2) flip-flop serpentine flow field (reproduced with permission from Ref. [80]). Schematics of (b1) conventional serpentine flow field, b2 serpentine flow field with the sloping channels, b3 serpentine flow field with the partially sloping channels and b4 serpentine flow field with the stepwise channels (reproduced with permission from Ref. [81]). c1 Schematics of conventional serpentine flow field and repatterned convection-enhanced flow field. c2 EE and EU with two flow fields under different flow rates and current densities (reproduced with permission from Ref. [36]). d1 Schematics of double spiral flow field with inlet/outlet at the center. d2 Efficiencies of the VRFBs with different flow fields (reproduced with permission from Ref. [82]) |
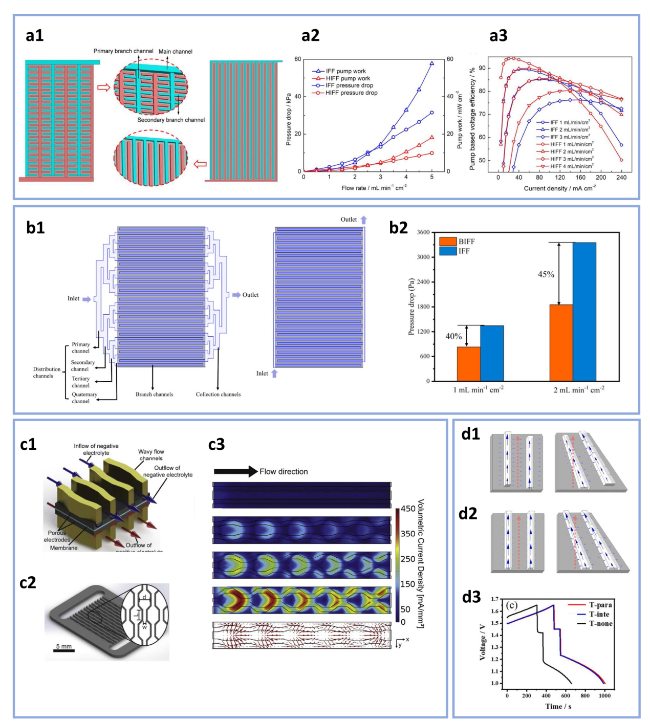
Fig. 10 a1 Schematics of the hierarchical interdigitated flow field and conventional interdigitated flow field. a2 Pressure drop and specific pumping loss of VRFBs with different flow fields. a3 VEpump of the VRFBs with different flow fields (reproduced with permission from Ref. [18]). b1 Schematics of the bifurcate interdigitated flow field and conventional interdigitated flow field. b2 Pressure drops of VRFBs with bifurcate interdigitated flow field and conventional interdigitated flow field (reproduced with permission from Ref. [84]). c1 Illustration of a section of the corrugated wall fluidic network. c2 Design of the 3D-printed fluidic network. c3 Volumetric current density distribution within the electrode and velocity arrows of cells with straight channels and corrugated channels (reproduced with permission from Ref. [85]). Schematics of rectangular flow field and trapezoid flow field with (d1) parallel channels and (d2) interdigitated channels. d3 Discharge curves of batteries with different flow fields at 200 mA cm−2 (reproduced with permission from Ref. [86]) |
Table 2 Brief description of novel flow fields performance |
| Author | Active area and operating conditions | Flow field | Battery performance |
|---|---|---|---|
| Gundlapalli et al. [80] | 900 cm2, 120 mA cm−2, 0.6 mL min−1 cm−2 | Serpentine | 67.6% SE |
| Flip-flop serpentine | 69.5% SE | ||
| Sun et al. [81] | 25 cm2, 100 mA cm−2, 30.0 mL min−1 | Serpentine | 65.1% SE |
| Stepwise serpentine | 68.9% SE | ||
| Wei et al. [36] | 9 cm2, 250 mA cm−2, 1.67 mL min−1 cm−2 | Serpentine | 65.3% EE |
| Convection-enhanced | 75.3% EE | ||
| Lu et al. [60] | 100 cm2, 40 mA cm−2, 1.2 mL min−1 cm−2 | Serpentine | 81.6% VEpump |
| Interdigitated | 84.9% VEpump | ||
| Rotary serpentine | 86.0% VEpump | ||
| Zeng et al. [18] | 40 cm2, 240 mA cm−2, 3.0 mL min−1 cm−2 | Interdigitated | 73.8% VEpump |
| Hierarchical interdigitated | 79.1% VEpump | ||
| Guo et al. [84] | 105 cm2, 250 mA cm−2, 2.4 mL min−1 cm−2 | Interdigitated | 69.95% VEpump |
| Bifurcate interdigitated | 73.10% VEpump | ||
| Lisboa et al. [85] | 100 mL min−1 high concentration solutions | Straight channels | 340 mW cm−2 power density |
| Corrugated channels | 875 mW cm−2 power density | ||
| Wan et al. [38] | 12.96 cm2, 200 mA cm−2, 3.0 mL min−1 cm−2 | Serpentine | 65.1% EE |
| Rotary serpentine | 76.0% EE |
Lisboa et al. investigated the flow fields using an alkaline quinone redox chemistry. In the other studies, the flow fields were compared using vanadium redox flow batteries |
3.2.2 Topology and machine learning assisted flow field pattern design
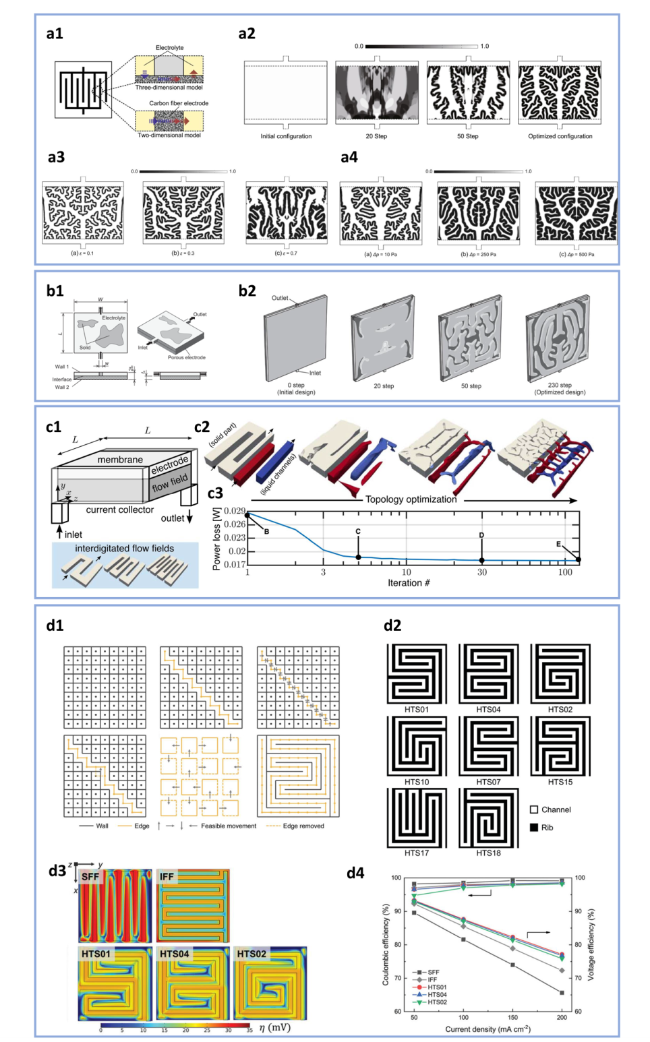
Fig. 11 a1 Comparison of flow field with respect to two- and three-dimensional analysis models in the case of an interdigitated flow field. a2 Optimization history of flow field configurations. Optimization configurations for different (a3) porosity settings and (a4) pressure drop settings (reproduced with permission from Ref. [37]). b1 Schematic of computational domain and boundary conditions. b2 Iteration history of topology-optimized flow fields (reproduced with permission from Ref. [88]). c1 Schematic of the half-cell computational domain. c2 Various design iterations during the optimization process. c3 The corresponding power loss during the optimization process (reproduced with permission from Ref. [89]). d1 Schematic of the key steps of the path generation algorithm. d2 Images of the eight promising flow fields selected from the screening process. d3 Simulated overpotential within the porous electrode. d4 CE and VE of the VRFBs with different flow fields (reproduced with permission from Ref. [38]) |
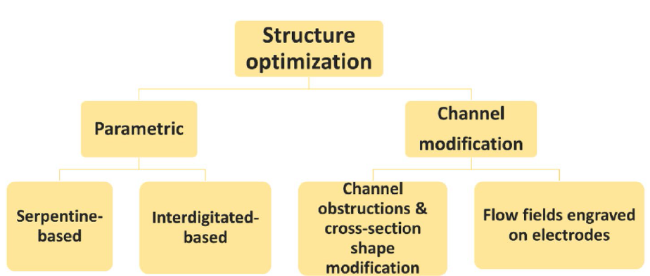
4 Flow field structure optimization
Fig. 12 Outlines for structure optimization of flow fields |
4.1 Parametric optimization
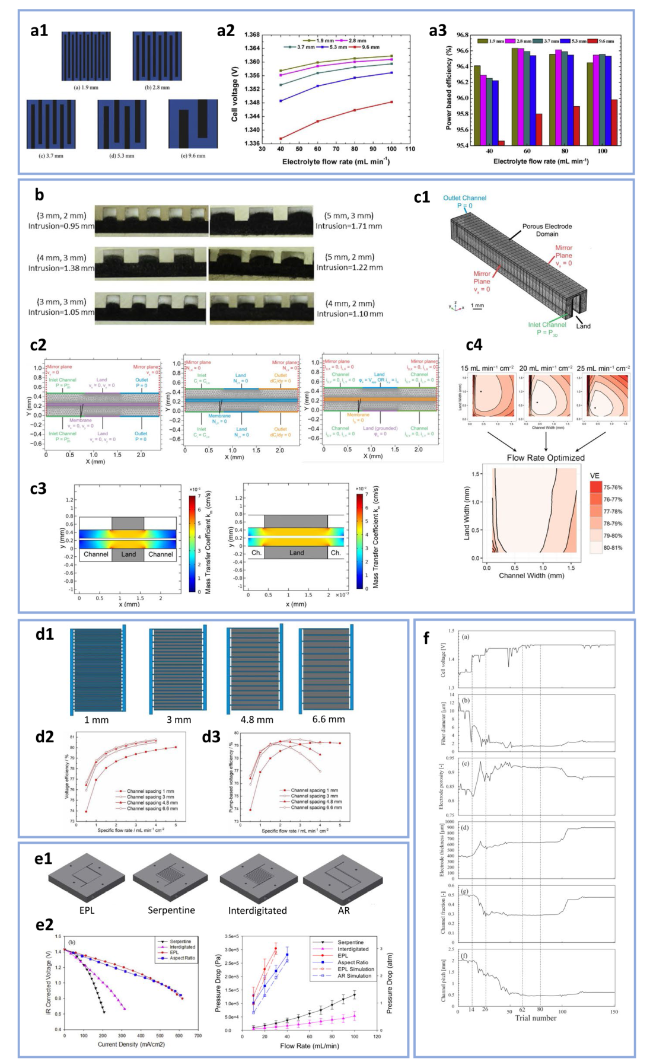
Fig. 13 a1 Schematics of five different serpentine flow fields. a2 Calculated cell voltage against the electrolyte flow rate and channel size. a3 Power-based efficiency according to the various flow rates and channel sizes (reproduced with permission from Ref. [40]). b Visualization of electrode intrusion into flow channels (reproduced with permission from Ref. [90]). c1 Boundary conditions for the three-dimensional fluid dynamics model. c2 Boundary conditions for the two-dimensional model coupling the fluid flow, mass transfer and electrochemical reactions. c3 Color map of the mass transfer coefficient in the “wide channel” (left) flow plate and “wide land” (right) flow plate. c4 Illustration of optimization on flow rate. The results from computations at various flow rates are combined to produce a single map of VEpump optimized with respect to flow rate (reproduced with permission from Ref. [92]). d1 The computational domain of interdigitated flow fields with different channel spacings. d2 VE and d3 VEpump of different channel spacings at a discharge current density of 200 mA cm−2 (reproduced with permission from Ref. [93]). e1 Flow field designs of Equal Path Length (EPL), Serpentine, Interdigitated and Aspect Ratio (AR) patterns. e2 Polarization curves and pressure drops of cells with different flow plates (reproduced with permission from Ref. [30]). f Values of various parameters and cell voltage during the multiple-parameter optimization process (reproduced with permission from Ref. [66]) |
4.2 Structure modification
4.2.1 Modification in flow channels
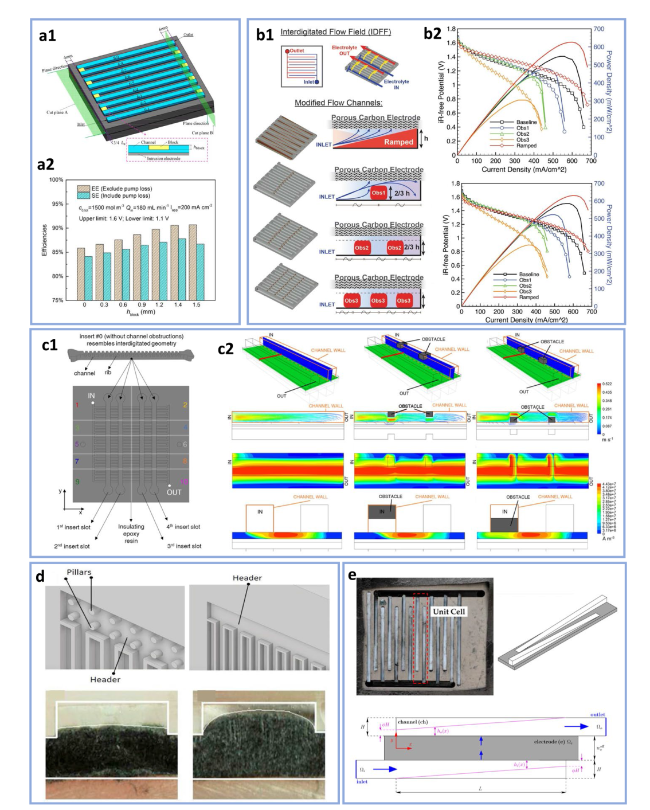
Fig. 14 Modification in flow channels. a1, a2 Serpentine flow channels modified with obstructions (reproduced with permission from Ref. [95]), b1, b2 interdigitated flow channels modified with ramps and obstructions (reproduced with permission from Ref. [97]), c1, c2 influence of locations and numbers of obstructions in interdigitated flow channels (reproduced with permission from Ref. [39]), d channels with pillars to avoid electrode intrusions (reproduced with permission from Ref. [98]). e tapered channel design for interdigitated flow field (reproduced with permission from Ref. [99]) |
4.2.2 Flow fields engraved on electrodes
Fig. 15 Flow fields engraved on electrodes. a Numerical analysis of engraving electrodes with cut-through interdigitated channels (reproduced with permission from Ref. [101]), b1, b2 engraving electrodes with a certain depth of different channel patterns (reproduced with permission from Ref. [102]), c electrodes with flow channels for scaled-up cells (reproduced with permission from Ref. [103]). d other patterns of flow channels engraved on electrodes (reproduced with permission from Ref. [104]), and e detached electrode-flow field design (reproduced with permission from Ref. [105]) |
5 Flow field scale-up
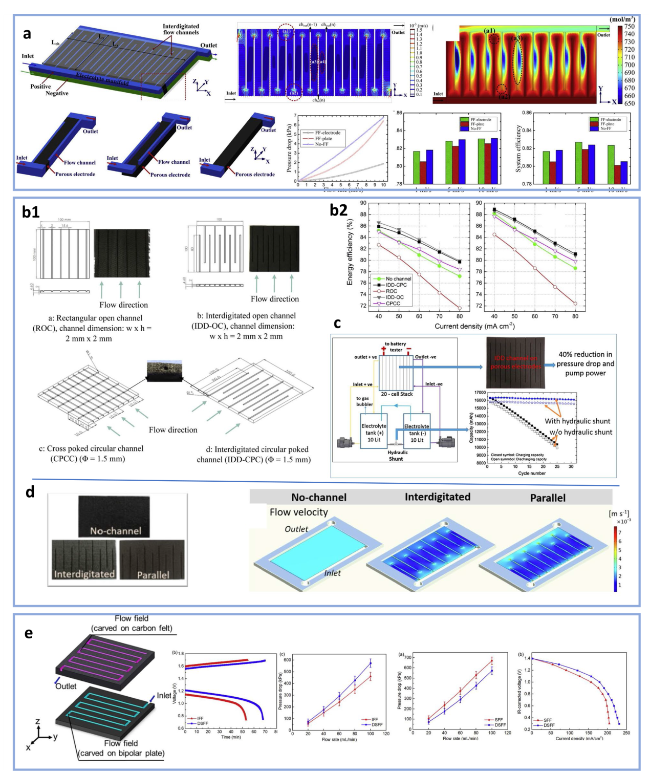
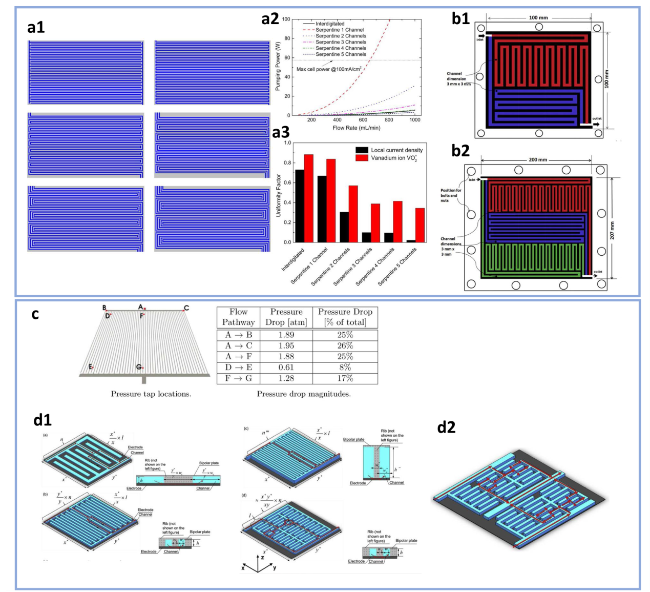
Fig. 16 Scaled-up strategies for serpentine- and interdigitated-based flow fields. a1, a2 Parallel splitting strategy for serpentine flow field (reproduced with permission from Ref. [23]), b1, b2 splitting serpentine flow field based on separate areas (reproduced with permission from Ref. [106]), c pressure distribution in interdigitated flow field (reproduced with permission from Ref. [46]), d1, d2 different pathways to scale-up flow fields (reproduced with permission from Ref. [32]) |